Înmulțirea matricelor în Python: Ghid complet
Acest ghid vă va familiariza cu procesul de înmulțire a două matrici folosind limbajul Python. Vom începe prin a analiza condițiile esențiale pentru o înmulțire validă a matricelor, apoi vom dezvolta o funcție personalizată Python pentru această operație. Mai târziu, vom explora cum se poate obține același rezultat folosind liste de înțelegere imbricate, pentru a încheia cu utilizarea NumPy și a funcțiilor sale integrate, optimizate pentru a efectua înmulțirea matricelor în mod eficient.
Verificarea validității înmulțirii matricelor
Înainte de a trece la codul Python, este important să revedem bazele înmulțirii matricelor. Aceasta este permisă doar când numărul coloanelor din prima matrice (A) este identic cu numărul rândurilor din a doua matrice (B).
Această condiție, întâlnită frecvent, este fundamentală datorită mecanismului înmulțirii matricelor. Imaginea de mai jos ilustrează acest aspect.
În acest exemplu generic, matricea A are dimensiunea m x n (m rânduri, n coloane), în timp ce matricea B are dimensiunea n x p (n rânduri, p coloane).
Forma matricei rezultate
Elementul de pe poziția (i, j) din matricea rezultată C este produsul scalar dintre rândul i din matricea A și coloana j din matricea B.
Calcularea unui element specific din matricea C implică calcularea produsului scalar al rândului și coloanei corespunzătoare din A și, respectiv, B.
Această operație, repetată pentru fiecare element, duce la obținerea matricei produs C, cu dimensiunea m x p (m rânduri, p coloane), după cum se poate observa.
Formula produsului scalar sau a produsului interior dintre doi vectori a și b este prezentată mai jos:

Rezumând, avem următoarele:
- Produsul scalar este definit exclusiv între vectori de lungime egală.
- Pentru validitatea produsului scalar dintre un rând și o coloană (în contextul înmulțirii a două matrici), ambele structuri trebuie să conțină același număr de elemente.
- În exemplul nostru, fiecare rând din matricea A are n elemente, la fel ca fiecare coloană din matricea B.
Așadar, ‘n’, reprezentând numărul de coloane din matricea A, coincide cu numărul de rânduri din matricea B, explicând astfel cerința ca aceste dimensiuni să fie egale pentru o înmulțire validă.
Sperăm că ați înțeles acum criteriile necesare pentru ca înmulțirea matricelor să fie validă și mecanismul de calcul al fiecărui element din matricea produs.
Să începem acum scrierea codului Python necesar pentru a înmulți două matrici.
Crearea unei funcții Python personalizate pentru înmulțirea matricelor
Vom începe cu crearea unei funcții personalizate pentru înmulțirea matricelor. Această funcție ar trebui să:
- Primească două matrici, A și B, ca argumente.
- Verifice validitatea înmulțirii dintre A și B.
- Dacă înmulțirea este validă, să returneze matricea produs C.
- Dacă nu este validă, să returneze un mesaj de eroare.
Pasul 1: Generăm două matrici cu numere întregi, folosind funcția `random.randint()` din NumPy. Alternativ, putem declara matricile ca liste imbricate Python.
import numpy as np
np.random.seed(27)
A = np.random.randint(1,10,size = (3,3))
B = np.random.randint(1,10,size = (3,2))
print(f"Matricea A:n {A}n")
print(f"Matricea B:n {B}n")
# Output
Matricea A:
[[4 9 9]
[9 1 6]
[9 2 3]]
Matricea B:
[[2 2]
[5 7]
[4 4]]
Pasul 2: Definim funcția `multiply_matrix(A,B)`. Această funcție primește matricile A și B ca intrări și returnează matricea produs C, dacă înmulțirea este posibilă.
def multiply_matrix(A,B):
global C
if A.shape[1] == B.shape[0]:
C = np.zeros((A.shape[0],B.shape[1]),dtype = int)
for row in range(A.shape[0]):
for col in range(B.shape[1]):
for elt in range(A.shape[1]):
C[row, col] += A[row, elt] * B[elt, col]
return C
else:
return "Înmulțirea matricelor A și B nu este posibilă."
Analiza definiției funcției
Să analizăm acum definiția funcției.
Declaram C ca variabilă globală: în mod implicit, variabilele definite în interiorul unei funcții Python au un domeniu de vizibilitate local și nu pot fi accesate din afara funcției. Pentru a face matricea C accesibilă extern, o declarăm ca variabilă globală, adăugând cuvântul cheie `global` înainte de numele variabilei.
Verificăm dacă înmulțirea matricelor este validă: folosim atributul `shape` pentru a verifica dacă înmulțirea dintre A și B este posibilă. Pentru orice matrice `arr`, `arr.shape[0]` și `arr.shape[1]` returnează numărul de rânduri și, respectiv, de coloane. Așadar, `A.shape[1] == B.shape[0]` verifică validitatea înmulțirii. Dacă această condiție este adevărată, se calculează matricea produs. În caz contrar, funcția returnează un mesaj de eroare.
Utilizăm bucle imbricate pentru calculul valorilor: pentru a calcula elementele matricei rezultate, iterăm prin rândurile matricei A, cu ajutorul buclei `for` exterioare. Bucla `for` interioară ne ajută să parcurgem coloanele matricei B, iar bucla `for` cea mai interioară ne permite să accesăm fiecare element al coloanei selectate.
▶️ Acum că am înțeles funcționarea funcției Python pentru înmulțirea matricelor, putem apela funcția cu matricile A și B pe care le-am generat anterior.
multiply_matrix(A,B)
# Output
array([[ 89, 107],
[ 47, 49],
[ 40, 44]])
Deoarece înmulțirea matricelor A și B este validă, funcția `multiply_matrix()` returnează matricea produs C.
Utilizarea listelor de înțelegere imbricate pentru înmulțirea matricelor
În secțiunea anterioară, ați învățat cum să creați o funcție Python pentru a înmulți matrice. Acum, vom analiza cum să obținem același rezultat folosind liste de înțelegere imbricate.
Iată lista de înțelegere imbricată pentru înmulțirea matricelor:
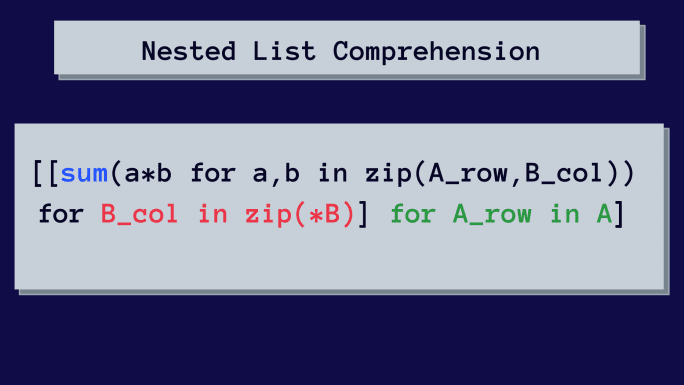
Deși poate părea complex la început, vom analiza lista de înțelegere pas cu pas.
Ne vom concentra pe o singură listă de înțelegere la un moment dat, identificând rolul ei.
Vom utiliza următorul model general pentru listele de înțelegere:
[<fa-asta> for <item> in <iterabil>] unde, <fa-asta>: operația sau expresia dorită <item>: fiecare element asupra căruia dorim să aplicăm operația <iterabil>: lista, tuplul etc. prin care iterăm
▶️ Pentru o înțelegere mai detaliată, vă recomandăm să consultați ghidul nostru despre listele de înțelegere în Python.
Rețineți că dorim să construim matricea rezultată C rând cu rând.
Explicația listei de înțelegere imbricate
Pasul 1: Calculăm o singură valoare în matricea C
Pentru un anumit rând ‘i’ din matricea A și o anumită coloană ‘j’ din matricea B, expresia de mai jos returnează valoarea de pe poziția (i, j) din matricea C.
sum(a*b for a,b in zip(A_row, B_col) # zip(A_row, B_col) returnează un iterator de tupluri # Dacă A_row = [a1, a2, a3] și B_col = [b1, b2, b3] # zip(A_row, B_col) va returna (a1, b1), (a2, b2), etc
Dacă i = j = 1, expresia va returna elementul c_11 din matricea C. Putem astfel obține un element dintr-un anumit rând.
Pasul 2: Construirea unui rând în matricea C
Următorul obiectiv este de a construi un rând întreg.
Pentru rândul 1 din matricea A, trebuie să iterăm prin toate coloanele din matricea B, obținând astfel un rând complet din matricea C.
Ne reîntoarcem la modelul de înțelegere a listei.
- Înlocuim
cu expresia de la pasul 1, reprezentând operația dorită. - Înlocuim
- cu `B_col`, reprezentând fiecare coloană din matricea B.
- Înlocuim
cu `zip(*B)`, lista care conține toate coloanele matricei B.
Astfel, obținem prima listă de înțelegere:
[sum(a*b for a,b in zip(A_row, B_col)) for B_col in zip(*B)] # zip(*B): * este operatorul de desfacere # zip(*B) returnează o listă cu coloanele matricei B
Pasul 3: Construirea tuturor rândurilor și obținerea matricei C
În continuare, populăm matricea produs C, calculând restul rândurilor.
Pentru aceasta, iterăm prin toate rândurile din matricea A.
Ne reîntoarcem la lista de înțelegere și facem următoarele:
- Înlocuim
cu lista de înțelegere de la pasul 2. Amintim că am calculat un rând întreg în pasul anterior. - Înlocuim
- cu `A_row` – fiecare rând din matricea A.
este matricea A în sine, în timp ce iterăm prin rândurile ei.
Iată lista de înțelegere finală: 🎉
[[sum(a*b for a,b in zip(A_row, B_col)) for B_col in zip(*B)]
for A_row in A]
Este timpul să verificăm rezultatul! ✔
# convertim într-un <a href="https://tipstrick.ro.com/numpy-reshape-arrays-in-python/">array NumPy</a> folosind np.array()
C = np.array([[sum(a*b for a,b in zip(A_row, B_col)) for B_col in zip(*B)]
for A_row in A])
# Output:
[[ 89 107]
[ 47 49]
[ 40 44]]
Observăm că aceasta este echivalentă cu buclele `for` imbricate pe care le-am utilizat anterior, dar într-o formă mai concisă.
Putem, de asemenea, eficientiza acest proces folosind funcții integrate. Să vedem cum în secțiunea următoare.
Folosirea funcției `NumPy matmul()` pentru înmulțirea matricelor în Python
Funcția `np.matmul()` primește două matrici ca intrări și returnează produsul lor, cu condiția ca înmulțirea dintre ele să fie validă.
C = np.matmul(A,B) print(C) # Output: [[ 89 107] [ 47 49] [ 40 44]]
Observăm că această metodă este mai simplă decât cele două prezentate anterior. De fapt, în loc de `np.matmul()`, putem folosi operatorul echivalent `@`, pe care îl vom vedea imediat.
Cum utilizăm operatorul `@` pentru înmulțirea matricelor în Python
În Python, `@` este un operator binar utilizat pentru înmulțirea matricelor. Se aplică la două matrici sau, mai general, la tablouri N-dimensionale NumPy și returnează matricea produs.
Notă: Pentru a folosi operatorul `@`, este necesar să aveți Python 3.5 sau o versiune ulterioară.
Iată cum îl puteți utiliza:
C = [email protected]
print(C)
# Output
array([[ 89, 107],
[ 47, 49],
[ 40, 44]])
Observăm că matricea produs C este identică cu cea obținută anterior.
Putem utiliza `np.dot()` pentru înmulțirea matricelor?
Dacă ați întâlnit cod care utilizează `np.dot()` pentru înmulțirea a două matrici, iată cum funcționează:
C = np.dot(A,B) print(C) # Output: [[ 89 107] [ 47 49] [ 40 44]]
Observăm că `np.dot(A, B)` returnează, de asemenea, matricea produs dorită.
Totuși, conform documentației NumPy, ar trebui să folosim `np.dot()` exclusiv pentru a calcula produsul scalar a doi vectori unidimensionali și nu pentru înmulțirea matricelor.
Reamintim, elementul de pe poziția (i, j) a matricei produs C este produsul scalar al rândului ‘i’ din matricea A și coloanei ‘j’ din matricea B.
Deoarece NumPy transmite implicit această operație de produs punctual la toate rândurile și coloanele, obținem matricea produs dorită. Dar, pentru a menține codul lizibil și a evita ambiguitățile, se recomandă utilizarea `np.matmul()` sau a operatorului `@`.
Concluzie
🎯 În acest ghid, am învățat următoarele:
- Condiția esențială pentru ca înmulțirea matricelor să fie validă: numărul de coloane din matricea A să fie egal cu numărul de rânduri din matricea B.
- Cum să scriem o funcție personalizată în Python care să verifice validitatea înmulțirii și să returneze matricea produs. Corpul funcției utilizează bucle `for` imbricate.
- Cum să utilizăm listele de înțelegere imbricate pentru a înmulți matrice. Deși mai concise decât buclele `for`, sunt mai greu de citit și înțeles.
- Cum să utilizăm funcția `NumPy` `np.matmul()` pentru a înmulți matrice, aceasta fiind cea mai eficientă din punct de vedere al vitezei.
- Despre operatorul `@` pentru înmulțirea matricelor în Python.
Acesta este finalul ghidului nostru despre înmulțirea matricelor în Python. Vă recomandăm să aprofundați cunoștințele și să învățați cum să verificați dacă un număr este prim în Python sau să rezolvați probleme interesante legate de șirurile de caractere.
Spor la învățat! 🎉