Identificarea și Gestionarea Vălorilor Aberante în Excel
O valoare aberantă, cunoscută și ca outlier, reprezintă o observație în datele tale care se distinge semnificativ, fie prin valoarea sa mult mai mare, fie mult mai mică decât restul datelor. În analiza datelor folosind Excel, aceste valori aberante pot distorsiona rezultatele, afectând acuratețea interpretărilor. De exemplu, media unui set de date poate fi influențată în mod nejustificat de prezența unor valori aberante. Din fericire, Excel oferă instrumente utile pentru a gestiona aceste anomalii. Vom explora împreună cum să le identificăm și să le tratăm.
Exemplu Simplificat
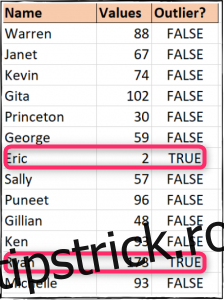
Într-un set de date mic, cum ar fi cel prezentat mai jos, identificarea valorilor aberante este intuitivă. Observăm imediat că valoarea „2” atribuită lui Eric și „173” atribuită lui Ryan sunt diferențe marcante față de restul valorilor. În cazul unui astfel de set de date, gestionarea manuală a acestor valori aberante este relativ simplă.
Însă, în cazul unor seturi de date ample, identificarea valorilor aberante devine mult mai dificilă. Capacitatea de a localiza aceste valori și de a le exclude din calculele statistice devine esențială pentru a obține rezultate relevante și precise. Vom examina în continuare modalitățile de a realiza acest lucru folosind Excel.
Pași pentru Identificarea Vălorilor Aberante
Pentru a identifica valorile aberante într-un set de date, vom urma acești pași:
1. Vom calcula primul și al treilea cuartil (Q1 și Q3), noțiuni pe care le vom explica în detaliu.
2. Vom determina intervalul intercuartilic (IQR), un alt concept pe care îl vom clarifica.
3. Vom calcula limitele superioare și inferioare ale intervalului nostru de date.
4. Vom folosi aceste limite pentru a identifica punctele de date care se încadrează în afara intervalului.
În exemplul nostru, vom utiliza o zonă de celule în dreapta datelor pentru a stoca aceste valori calculate, așa cum se vede în imaginea de mai jos.
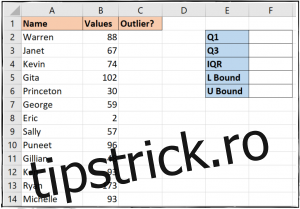
Să începem analiza.
Pasul Unu: Calculul Quartilelor
Dacă împărțim un set de date ordonat în patru părți egale, fiecare parte reprezintă un cuartil. Primul cuartil (Q1) reprezintă cele mai mici 25% dintre valori, al doilea cuartil (Q2) cuprinde următoarele 25%, și așa mai departe. Această etapă este crucială, deoarece valorile aberante sunt adesea definite ca fiind cele care se află la mai mult de 1,5 * IQR sub Q1 sau la mai mult de 1,5 * IQR deasupra Q3. Pentru a determina aceste valori aberante, trebuie mai întâi să calculăm quartilele.
Excel oferă funcția QUARTILE pentru calculul cuartilelor. Aceasta necesită două argumente: matricea (intervalul de date) și numărul cuartilului (1, 2, 3 sau 4).
=QUARTILE(matrice, cuart)
Matricea este intervalul valorilor pe care le analizăm, iar cuart este un număr care indică cuartilul dorit (1 pentru primul cuartil, 2 pentru al doilea, etc.).
Notă: Începând cu Excel 2010, Microsoft a introdus funcțiile QUARTILE.INC și QUARTILE.EXC ca îmbunătățiri ale funcției QUARTILE. Cu toate acestea, QUARTILE este mai compatibil cu versiunile mai vechi, ceea ce îl face potrivit pentru lucrul în diferite medii Excel.
Să revenim la exemplul nostru:

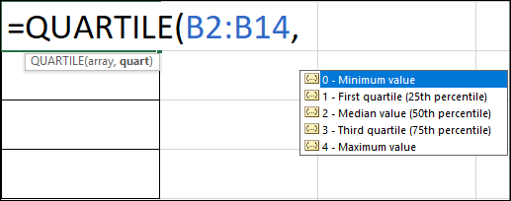
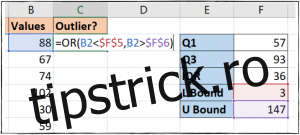
Pentru a calcula primul cuartil, vom introduce următoarea formulă în celula F2:
=QUARTILE(B2:B14,1)
Pe măsură ce introducem formula, Excel oferă o listă de opțiuni pentru argumentul „cuart”.
Pentru a calcula al treilea cuartil, vom introduce o formulă similară în celula F3, dar vom folosi 3 în loc de 1.
=QUARTILE(B2:B14,3)
Acum, avem quartilele afișate în celule.

Pasul Doi: Calculul Intervalului Intercuartilic
Intervalul intercuartilic (IQR) reprezintă diferența dintre al treilea și primul cuartil, acoperind 50% dintre valorile centrale ale datelor. Se calculează prin scăderea valorii primului cuartil din valoarea celui de-al treilea cuartil.
Vom folosi o formulă simplă în celula F4, scăzând primul cuartil din al treilea:
=F3-F2
Acum, avem afișat intervalul intercuartilic.

Pasul Trei: Stabilirea Limitelor Inferioare și Superioare
Limitele inferioare și superioare delimitează intervalul de date considerat „normal”. Orice valoare care se află în afara acestor limite este considerată o valoare aberantă.
Pentru a calcula limita inferioară în celula F5, vom înmulți IQR cu 1,5 și apoi vom scădea rezultatul din Q1:
=F2-(1.5*F4)
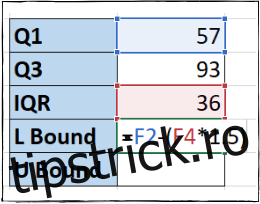
Notă: Parantezele din formulă nu sunt necesare, deoarece înmulțirea este efectuată înainte de scădere, dar ele fac formula mai ușor de citit.
Pentru a calcula limita superioară în celula F6, vom înmulți IQR cu 1,5 și vom adăuga rezultatul la Q3:
=F3+(1.5*F4)
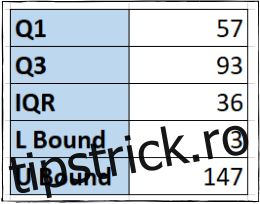
Pasul Patru: Identificarea Vălorilor Aberante
Acum că am stabilit toate valorile de bază, putem identifica valorile aberante, adică acele puncte de date care sunt mai mici decât limita inferioară sau mai mari decât limita superioară.
Vom utiliza funcția SAU pentru a realiza un test logic și a evidenția valorile care respectă criteriile noastre. Vom introduce următoarea formulă în celula C2:
=OR(B2F$6)
Apoi vom copia această formulă în celulele C3-C14. O valoare TRUE indică o valoare aberantă și, după cum putem observa, avem două astfel de valori în setul nostru de date.
Ignorarea Valorilor Aberante la Calculul Mediei
Metoda de identificare a valorilor aberante folosind funcția QUARTILE și intervalul intercuartilic este una dintre cele mai comune. Cu toate acestea, atunci când dorim să calculăm media unui set de valori, eliminând influența valorilor aberante, există o funcție mai rapidă și mai directă. Această funcție nu identifică explicit valorile aberante, dar permite o mai mare flexibilitate în ajustarea datelor.
Funcția pe care o vom utiliza se numește TRIMMEAN, iar sintaxa ei este următoarea:
=TRIMMEAN(matrice, procent)
Matricea este intervalul de valori pentru care dorim să calculăm media, iar procentul este procentul de valori pe care dorim să le excludem din capetele superioare și inferioare ale intervalului (putem introduce valoarea ca procent sau zecimală).
În exemplul nostru, am introdus următoarea formulă în celula D3 pentru a calcula media, excluzând 20% din valori aberante:
=TRIMMEAN(B2:B14, 20%)
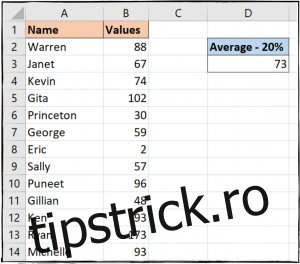
Astfel, avem la dispoziție două modalități diferite de gestionare a valorilor aberante. Indiferent dacă dorim să le identificăm pentru a le analiza mai profund sau să le excludem din calcule pentru a obține rezultate mai precise, Excel ne pune la dispoziție funcțiile necesare.