Acest ghid detaliat vă va familiariza cu utilizarea funcției `linspace()` din biblioteca NumPy pentru a genera secvențe de numere echidistante în Python.
Veți explora sintaxa `linspace()` și veți parcurge exemple practice pentru a înțelege funcționalitatea acesteia.
Rețineți: Pentru a beneficia de acest tutorial, trebuie să aveți instalate Python și NumPy.
Dacă nu aveți încă NumPy, am pregătit un ghid rapid pentru instalare.
Să începem explorarea!
Instalarea și importarea NumPy
Înainte de a începe, să recapitulăm rapid etapele necesare pentru a instala biblioteca NumPy.
⏩ Dacă aveți deja instalat NumPy, puteți trece direct la secțiunea următoare.
- Dacă folosiți Google Colab, un mediu Jupyter notebook bazat pe cloud, puteți importa NumPy și începe imediat programarea. (Această metodă este recomandată pentru acest tutorial ✅)
- Pentru a configura un mediu de lucru local, recomand instalarea distribuției Anaconda de Python. Aceasta include o mulțime de pachete utile preinstalate. Puteți descărca instalatorul potrivit pentru sistemul dvs. de operare. Configurarea durează doar câteva minute. ⌛
- Chiar dacă aveți deja Python instalat, puteți instala distribuția Anaconda. Utilizați `conda` sau `pip` pentru a instala și gestiona pachetele. Executați una dintre următoarele comenzi în linia de comandă Anaconda pentru a instala NumPy:
# Instalați NumPy folosind conda conda install numpy # Instalați NumPy folosind pip pip install numpy
Următorul pas este importarea NumPy sub aliasul `np`. Aceasta vă permite să faceți referire la NumPy folosind `np`, evitând să scrieți `numpy` de fiecare dată când accesați un membru al modulului.
import numpy as np
În continuare, vom utiliza notația cu puncte pentru a accesa diversele funcții din biblioteca NumPy, în felul următor: `np.nume_funcție`.
Importanța numerelor echidistante
În lucrul cu matricele NumPy, adesea este necesară crearea unei matrice de numere cu distanță egală într-un interval dat.
Înainte de a continua, să recapitulăm rapid funcția similară `np.arange()`.
Comparație: NumPy `linspace()` vs. NumPy `arange()`
Dacă ați mai utilizat NumPy, probabil ați folosit `np.arange()` pentru a crea o secvență de numere într-un interval specific.
Știți că `np.arange(start, stop, step)` generează o serie de numere de la `start` până la `stop` (exclusiv), cu un pas dat, implicit 1.
Totuși, valoarea pasului nu este întotdeauna evidentă. Să vedem de ce.
De exemplu, dacă aveți nevoie de 4 numere echidistante între 0 și 1, știți că pasul este 0.25. Dar, cum `np.arange()` exclude valoarea de oprire 1, veți fi nevoit să alegeți un interval care depășește valoarea dorită.
Următoarea imagine ilustrează alte câteva exemple în care aveți nevoie de un anumit număr de puncte echidistante în intervalul [a, b].
Puncte echidistante într-un interval
În exemplul inițial, obținerea a 4 puncte echidistante între 0 și 1 a fost simplă, cu un pas de 0.25.
Dar, dacă doriți 7 puncte echidistante între 1 și 33, pasul poate să nu fie imediat evident. În acest caz, puteți calcula manual valoarea pasului.
Din fericire, `np.linspace()` face acest lucru și mai simplu! 😄

Când utilizați `np.linspace()`, specificați numărul de puncte dorite în interval, fără a fi nevoie să calculați pasul. Veți primi exact matricea de care aveți nevoie.
Cu această înțelegere, să continuăm să analizăm sintaxa funcției `linspace()` în secțiunea următoare.
Sintaxa `linspace()` din NumPy
Sintaxa funcției `linspace()` din NumPy este prezentată mai jos:
np.linspace(start, stop, num, endpoint, retstep, dtype, axis)
La prima vedere, sintaxa poate părea complexă, cu mulți parametri.
Totuși, majoritatea parametrilor sunt opționali, iar vom ajunge la o sintaxă mai simplă în scurt timp.
Să analizăm sintaxa mai detaliat:
- `start` și `stop` sunt valorile de început și, respectiv, de sfârșit ale intervalului. Atât `start`, cât și `stop` pot fi scalari sau matrice. În acest tutorial, ne vom concentra pe valorile scalare.
- `num` este numărul de puncte echidistante. Este un parametru opțional, cu o valoare implicită de 50.
- `endpoint` este, de asemenea, un parametru opțional care poate fi `True` sau `False`. Valoarea implicită este `True`, ceea ce înseamnă că punctul final este inclus în interval. Îl puteți seta la `False` pentru a exclude punctul final.
- `retstep` este un alt parametru opțional boolean. Când este setat la `True`, returnează și valoarea pasului.
- `dtype` este tipul de date al numerelor din matrice. Tipul este de obicei dedus ca `float` și nu trebuie specificat explicit.
- `axis` este un alt parametru opțional care indică axa de-a lungul căreia sunt stocate numerele. Acesta este relevant doar când valorile `start` și `stop` sunt ele însele matrice.
▶️ Ce returnează `np.linspace()`?
Returnează o matrice N-dimensională cu numere echidistante. Dacă parametrul `retstep` este `True`, returnează și dimensiunea pasului.
Pe baza discuției de până acum, iată o sintaxă simplificată pentru a utiliza `np.linspace()`:
np.linspace(start, stop, num)
Această linie de cod returnează o matrice cu `num` numere echidistante în intervalul [start, stop].
Acum că am înțeles sintaxa, să începem să scriem exemple.
Cum se creează matrice echidistante cu `linspace()` din NumPy
#1. În primul exemplu, creăm o matrice cu 20 de numere echidistante în intervalul [1, 5].
Puteți specifica valorile `start`, `stop` și `num` ca argumente cu nume. Acest lucru este demonstrat în codul de mai jos:
import numpy as np arr1 = np.linspace(start = 1,stop = 5,num = 20) print(arr1) # Ieșire: [1. 1.21052632 1.42105263 1.63157895 1.84210526 2.05263158 2.26315789 2.47368421 2.68421053 2.89473684 3.10526316 3.31578947 3.52631579 3.73684211 3.94736842 4.15789474 4.36842105 4.57894737 4.78947368 5. ]
Observați cum numerele din matrice încep cu 1 și se termină cu 5, incluzând ambele capete. De asemenea, observați că numerele, inclusiv 1 și 5, sunt reprezentate ca valori `float`.
#2. În exemplul anterior, ați folosit valorile pentru `start`, `stop` și `num` ca argumente numite. Dacă introduceți argumentele în ordinea corectă, le puteți folosi direct ca argumente de poziție, așa cum se arată mai jos.
import numpy as np arr2 = np.linspace(1,5,20) print(arr2) # Ieșire: [1. 1.21052632 1.42105263 1.63157895 1.84210526 2.05263158 2.26315789 2.47368421 2.68421053 2.89473684 3.10526316 3.31578947 3.52631579 3.73684211 3.94736842 4.15789474 4.36842105 4.57894737 4.78947368 5. ]
#3. Acum, să creăm o altă matrice în care setăm `retstep` la `True`.
Aceasta înseamnă că funcția returnează acum atât matricea, cât și pasul. Putem despacheta aceste valori în două variabile: `arr3` pentru matrice și `step_size` pentru dimensiunea pasului.
Următorul cod demonstrează cum:
import numpy as np arr3, step_size = np.linspace(1,5,20,retstep = True) print(arr3) # Ieșire: [1. 1.21052632 1.42105263 1.63157895 1.84210526 2.05263158 2.26315789 2.47368421 2.68421053 2.89473684 3.10526316 3.31578947 3.52631579 3.73684211 3.94736842 4.15789474 4.36842105 4.57894737 4.78947368 5. ] # Ieșire: print(step_size) 0.21052631578947367
#4. Ca ultim exemplu, vom seta parametrul `endpoint` la `False` și vom vedea ce se întâmplă.
import numpy as np arr4 = np.linspace(1,5,20,endpoint = False) print(arr4) # Ieșire: [1. 1.2 1.4 1.6 1.8 2. 2.2 2.4 2.6 2.8 3. 3.2 3.4 3.6 3.8 4. 4.2 4.4 4.6 4.8]
În matricea returnată, se poate observa că 1 este inclus, în timp ce 5 este exclus. Ultima valoare din matrice este 4.8, dar avem tot 20 de numere.
Până acum, am generat doar matrice de numere echidistante. În secțiunea următoare, vom vizualiza aceste numere folosind grafice.
Cum se vizualizează numerele echidistante într-un interval
În această secțiune, vom utiliza intervalul [10, 15]. Vom genera două matrice folosind `np.linspace()`, cu 8 și respectiv 12 puncte.
După ce am generat matricele, putem utiliza funcția de graficare din biblioteca Matplotlib pentru a le reprezenta vizual.
Pentru claritate, cele două rețele de N1 = 8 și N2 = 12 puncte echidistante vor fi reprezentate pe axa y, la poziții diferite.
Următorul cod demonstrează acest lucru:
import numpy as np
import matplotlib.pyplot as plt
N1 = 8
N2 = 12
a = 10
b = 15
y1 = np.zeros(N1)
y2 = np.zeros(N2)
x1 = np.linspace(a, b, N1)
x2 = np.linspace(a, b, N2)
plt.plot(x1, y1-0.5, 'o')
plt.plot(x2, y2 + 0.5, 'o')
plt.ylim([-1, 1])
plt.title(f'Numere echidistante în intervalul [{a},{b}]')
plt.xlabel('Interval')
plt.show()
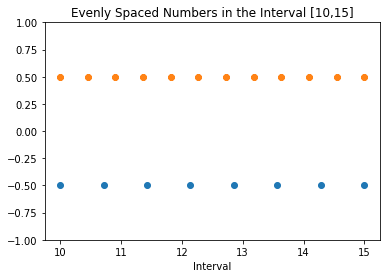
Generarea de puncte echidistante poate fi utilă când lucrați cu funcții matematice. Vom explora acest aspect în secțiunea următoare.
Cum se utilizează `linspace()` cu funcții matematice
Odată ce ați generat o matrice de numere echidistante folosind `np.linspace()`, puteți calcula valorile funcțiilor matematice pe acel interval.
În codul de mai jos, generăm mai întâi 50 de puncte echidistante în intervalul de la 0 la 2π. Apoi creăm matricea `y` aplicând `np.sin()` pe matricea `x`. Rețineți că puteți omite parametrul `num` deoarece valoarea implicită este 50. Îl vom folosi explicit în continuare.
Pasul următor este vizualizarea funcției sinus în intervalul [0, 2π]. Pentru a face acest lucru, puteți folosi biblioteca matplotlib, ca în exemplul anterior. Mai specific, funcția `plot()` din `matplotlib.pyplot` este folosită pentru a crea un grafic de linii.
import numpy as np
import matplotlib.pyplot as plt
N = 50
a = 0.0
b = 2*np.pi
x = np.linspace(a, b, N)
y = np.sin(x)
plt.plot(x, y, marker = "o")
plt.ylim([-1, 1])
plt.title(f'y = sin(x)')
plt.xlabel('x ---->')
plt.show()
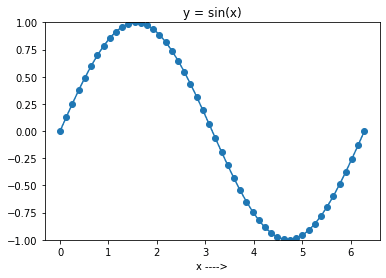
Acum rulați codul de mai sus setând N la 10. Veți obține graficul din imaginea de mai jos.
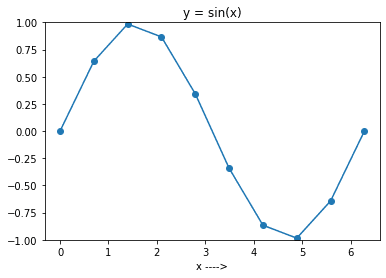
Se observă că graficul nu este foarte neted, deoarece am inclus doar 10 puncte în interval.
În general, cu cât numărul de puncte luate în considerare este mai mare, cu atât graficul funcției va fi mai fin.
Concluzie
Iată un rezumat al ceea ce am învățat:
- `np.linspace(start, stop, num)` returnează o matrice cu `num` numere echidistante în intervalul [start, stop].
- Setați parametrul opțional `endpoint` la `False` pentru a exclude valoarea de oprire și a obține intervalul [start, stop).
- Setați opțional `retstep` la `True` pentru a obține dimensiunea pasului.
- Generați matrice echidistante folosind `np.linspace()` și folosiți matricea cu funcții matematice.
Sperăm că acum ați înțeles cum funcționează funcția `np.linspace()`. Puteți alege să rulați exemplele de mai sus în blocnotesul Jupyter. Consultați ghidul nostru despre blocnotesul Jupyter sau alte alternative Jupyter pe care le puteți lua în considerare.
Ne vedem în curând într-un alt tutorial Python. Până atunci, continuați să programați! 😀