În universul programării, structurile de date reprezintă elemente fundamentale. Ele ne ajută să organizăm informațiile într-un mod eficient și logic. Printre cele mai simple structuri de date se numără stiva.
Haideți să explorăm conceptul de stivă și modul în care poate fi implementată în limbajul Python.
Ce este, de fapt, o stivă?
O stivă se aseamănă cu un teanc de cărți sau un șir de scaune din viața reală. Ea operează pe baza principiului „Ultimul intrat, primul ieșit” (LIFO – Last-In/First-Out). Fiind una dintre cele mai simple structuri de date, este important să o înțelegem printr-un exemplu concret.
Imaginați-vă un teanc de cărți.
Pentru a ajunge la a treia carte de sus, trebuie să eliminăm primele două cărți. Astfel, cartea așezată ultima în teanc va fi prima luată de acolo. Stiva, ca structură de date, urmează același principiu LIFO în programare.
Operații fundamentale ale unei stive
Într-o stivă, există în principal două operații cheie:
1. push(element)
Aceasta este operația de adăugare a unui element în vârful stivei.
2. pop()
Aceasta este operația de eliminare a elementului aflat în vârful stivei.
Mai jos puteți vedea ilustrații ale operațiilor push și pop.
În plus, vom defini câteva funcții ajutătoare care ne vor oferi informații suplimentare despre stivă.
Să le analizăm:
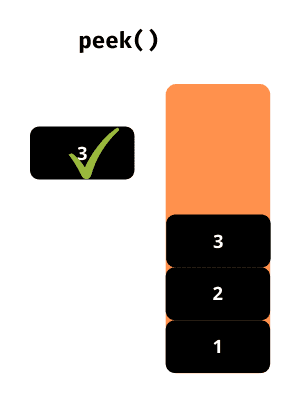
peek()
Această funcție returnează elementul situat în vârful stivei, fără a-l elimina.
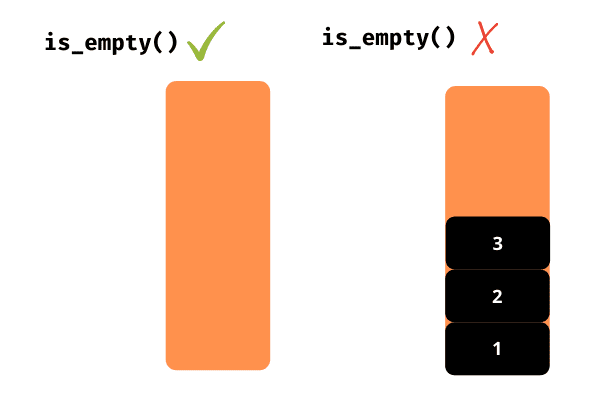
is_empty()
Această funcție ne indică dacă stiva este goală sau nu, returnând o valoare booleană (True sau False).
Am acoperit aspectele teoretice ale structurii de date stivă. Acum, să trecem la implementarea practică, fără alte introduceri.
Vom presupune că aveți instalat Python pe calculator. Dacă nu, puteți utiliza un compilator online.
Implementarea stivei în Python
Implementarea stivei este relativ simplă în comparație cu alte structuri de date. Există mai multe moduri de a realiza acest lucru în Python.
Să le explorăm pe rând:
#1. Utilizarea listelor
Vom implementa stiva folosind o listă într-o clasă. Să analizăm pașii acestei implementări:
Pasul 1: Definim o clasă numită „Stack”.
class Stack: pass
Pasul 2: Stocăm datele într-o listă. Adăugăm o listă goală ca atribut al clasei „Stack”.
class Stack: def __init__(self): self.elements = []
Pasul 3: Pentru a adăuga elemente în stivă, creăm o metodă „push”, care primește ca argument data și o adaugă la lista de elemente.
class Stack: def __init__(self): self.elements = [] def push(self, data): self.elements.append(data) return data
Pasul 4: Similar, definim metoda „pop” pentru a elimina elementul din vârful stivei, folosind metoda „pop” a listei.
class Stack: ## ... def pop(self): return self.elements.pop()
Am finalizat implementarea stivei cu operațiile de bază. Acum, haideți să adăugăm funcțiile ajutătoare pentru a obține mai multe informații despre stivă.
Pasul 5: Elementul din vârful stivei poate fi accesat folosind indexul negativ. Astfel, elementul de cod [-1] returnează ultimul element din listă, care este elementul din vârful stivei.
class Stack: ## ... def peek(self): return self.elements[-1]
Pasul 6: Dacă lungimea listei este 0, stiva este considerată goală. Implementăm metoda care ne indică dacă stiva este goală.
class Stack: ## ... def is_empty(self): return len(self.elements) == 0
Am terminat implementarea stivei folosind o listă.
Dar, cum folosim stiva implementată? Trebuie să creăm un obiect din clasa Stack. Să facem asta!
class Stack:
## ...
if __name__ == '__main__':
stack = Stack()
Am creat obiectul „stack” și suntem gata să îl folosim. Să urmăm pașii de mai jos pentru a testa operațiile stivei:
- Verificăm dacă stiva este goală, folosind metoda is_empty. Ar trebui să returneze True.
- Adăugăm elementele 1, 2, 3, 4, 5 în stivă folosind metoda push.
- Metoda is_empty ar trebui să returneze False. Verificăm.
- Afișăm elementul din vârful stivei folosind metoda peek.
- Eliminăm elementul din vârful stivei folosind metoda pop.
- Verificăm din nou elementul din vârf, folosind peek. Ar trebui să returneze 4.
- Eliminăm toate elementele din stivă.
- Metoda is_empty ar trebui să returneze True. Verificăm.
Implementarea stivei este corectă dacă trecem de toți pașii de mai sus. Încercați să scrieți codul corespunzător acestor pași.
Ați scris codul? Nu vă faceți griji, consultați codul de mai jos:
class Stack:
def __init__(self):
self.elements = []
def push(self, data):
self.elements.append(data)
return data
def pop(self):
return self.elements.pop()
def peek(self):
return self.elements[-1]
def is_empty(self):
return len(self.elements) == 0
if __name__ == '__main__':
stack = Stack()
## checking is_empty method -> true
print(stack.is_empty())
## pushing the elements
stack.push(1)
stack.push(2)
stack.push(3)
stack.push(4)
stack.push(5)
## again checking is_empty method -> false
print(stack.is_empty())
## printing the topmost element of the stack -> 5
print(stack.peek())
## popping the topmost element -> 5
stack.pop()
## checking the topmost element using peek method -> 4
print(stack.peek())
## popping all the elements
stack.pop()
stack.pop()
stack.pop()
stack.pop()
## checking the is_empty method for the last time -> true
print(stack.is_empty())
Am finalizat cu succes implementarea stivei de la zero folosind o listă! Dacă rulați codul de mai sus, veți obține rezultatul de mai jos:
True False 5 4 True
Putem folosi direct o listă ca stivă. Totuși, implementarea anterioară ne ajută să înțelegem cum se implementează stiva în alte limbaje de programare.
Vă recomand să consultați și articolele despre liste.
Să vedem acum cum putem folosi „deque” din modulul „collections”, care poate fi folosit și ca stivă.
#2. Utilizarea „deque” din modulul „collections”
„deque” (double-ended queue) este implementat ca o coadă bidirecțională. Având posibilitatea de a adăuga și elimina elemente de la ambele capete, îl putem utiliza ca o stivă, respectând principiul LIFO.
Este implementat folosind o listă dublu înlănțuită, ceea ce înseamnă că performanța operațiilor de inserare și eliminare este constantă. Accesarea elementelor din mijlocul listei dublu înlănțuite necesită timp O(n). Însă, în cazul stivelor, nu este necesar să accesăm elementele din mijloc.
Înainte de implementarea stivei, să vedem metodele „deque” pe care le vom utiliza:
- append(data) – folosită pentru a adăuga elemente în stivă.
- pop() – folosită pentru a elimina elementul din vârful stivei.
Nu avem metode alternative pentru „peek” și „is_empty”. Putem afișa întreaga stivă în loc de „peek” și putem folosi metoda „len” pentru a verifica dacă stiva este goală.
Să implementăm stiva folosind „deque” din modulul „collections”:
from collections import deque ## creating deque object stack = deque() ## checking whether stack is empty or not -> true print(len(stack) == 0) ## pushing the elements stack.append(1) stack.append(2) stack.append(3) stack.append(4) stack.append(5) ## again checking whether stack is empty or not -> false print(len(stack) == 0) ## printing the stack print(stack) ## popping the topmost element -> 5 stack.pop() ## printing the stack print(stack) ## popping all the elements stack.pop() stack.pop() stack.pop() stack.pop() ## checking the whether stack is empty or not for the last time -> true print(len(stack) == 0)
Am învățat cum să implementăm o stivă folosind „deque”. Dacă executați codul de mai sus, veți obține rezultatul de mai jos:
True False deque([1, 2, 3, 4, 5]) deque([1, 2, 3, 4]) True
Am văzut până acum două moduri de a implementa o stivă. Mai există și alte modalități? Da! Să vedem ultimul mod de implementare a unei stive în acest tutorial.
#3. Utilizarea „LifoQueue” din modulul „queue”
Numele „LifoQueue” indică faptul că urmează principiul LIFO. Prin urmare, îl putem folosi ca stivă. Este parte a modulului încorporat „queue”. „LifoQueue” oferă câteva metode utile:
- put(data) – adaugă sau „împinge” datele în coadă.
- get() – elimină elementul din vârful cozii.
- empty() – returnează „True” dacă coada este goală, altfel „False”.
- qsize() – returnează dimensiunea cozii.
Să implementăm o stivă folosind „LifoQueue”:
from queue import LifoQueue
## creating LifoQueue object
stack = LifoQueue()
## checking whether stack is empty or not -> true
print(stack.empty())
## pushing the elements
stack.put(1)
stack.put(2)
stack.put(3)
stack.put(4)
stack.put(5)
## again checking whether stack is empty or not -> false
print(stack.empty())
## popping all the elements
print(stack.get())
print(stack.get())
print(stack.get())
## checking the stack size
print("Size", stack.qsize())
print(stack.get())
print(stack.get())
## checking the whether stack is empty or not for the last time -> true
print(stack.empty())
Dacă executați codul de mai sus, veți obține următorul rezultat:
True False 5 4 3 Size 2 2 1 True
Aplicații practice ale stivei
Acum că aveți o înțelegere solidă a conceptului de stivă, puteți începe să îl aplicați în diverse probleme de programare. Să vedem o problemă concretă și să o rezolvăm cu ajutorul unei stive.
Dându-se o expresie, scrieți un program care verifică dacă parantezele, acoladele și parantezele drepte sunt echilibrate corect.
Exemple:
Intrare: „[{}]([])”
Ieșire: echilibrată
Intrare: „{[}]([])”
Ieșire: neechilibrată
Putem folosi o stivă pentru a rezolva această problemă. Iată pașii:
- Creăm o stivă pentru a stoca caracterele.
- Dacă lungimea expresiei este impară, expresia nu este echilibrată.
- Iterăm prin expresia dată.
- Dacă caracterul curent este o paranteză deschisă (sau { sau [, îl adăugăm în stivă.
- Dacă caracterul curent este o paranteză închisă ) sau } sau ], eliminăm elementul din vârful stivei.
- Dacă paranteza eliminată se potrivește cu paranteza curentă, continuăm; altfel, parantezele nu sunt echilibrate.
- După iterare, dacă stiva este goală, expresia este echilibrată; altfel, nu este echilibrată.
Putem folosi un set pentru a verifica dacă parantezele se potrivesc corect.
## stack
class Stack:
def __init__(self):
self.elements = []
def push(self, data):
self.elements.append(data)
return data
def pop(self):
return self.elements.pop()
def peek(self):
return self.elements[-1]
def is_empty(self):
return len(self.elements) == 0
def balance_check(expression):
## checking the length of the expression
if len(expression) % 2 != 0:
## not balanced if the length is odd
return False
## for checking
opening_brackets = set('([{')
pairs = set([ ('(',')'), ('[',']'), ('{','}') ])
## stack initialization
stack = Stack()
## iterating through the given expression
for bracket in expression:
## checking whether the current bracket is opened or not
if bracket in opening_brackets:
## adding to the stack
stack.push(bracket)
else:
## popping out the last bracket from the stack
popped_bracket = stack.pop()
## checking whether popped and current bracket pair
if (popped_bracket, bracket) not in pairs:
return False
return stack.is_empty()
if __name__ == '__main__':
if balance_check('[{}]([])'):
print("Balanced")
else:
print("Not Balanced")
if balance_check('{[}]([])'):
print("Balanced")
else:
print("Not Balanced")
Stiva poate fi aplicată și în multe alte probleme. Exemplul de mai sus este doar unul dintre ele. Încercați să aplicați conceptul de stivă în situațiile în care considerați că este cel mai potrivit.
Concluzii
Felicitări! Ați ajuns la finalul acestui tutorial. Sper că v-a plăcut la fel de mult pe cât mi-a plăcut mie să îl creez. Acesta a fost tutorialul.
Spor la codat! 🙂 👨💻