Cum să imprimați triunghiul lui Pascal în Python

de
Tweet
Share
Share
Pin

Acest tutorial vă va învăța cum să imprimați triunghiul lui Pascal în Python pentru un anumit număr de rânduri.

Veți începe prin a învăța cum să construiți triunghiul lui Pascal. Apoi veți continua să scrieți o funcție Python și veți învăța să o optimizați în continuare.

▶️ Să începem!

Ce este triunghiul lui Pascal și cum se construiește?

Imprimarea triunghiului lui Pascal pentru un anumit număr de rânduri este o întrebare populară de interviu.

În triunghiul lui Pascal cu n rânduri, rândul numărul i are i elemente.

Deci primul rând are un element și este 1. Și fiecare element din rândurile următoare este suma celor două numere aflate direct deasupra lui.

Următoarea figură explică cum se construiește triunghiul lui Pascal cu cinci rânduri.

Triunghiul lui Pascal pentru numRows = 5 (Imaginea autorului)

Observați cum puteți introduce zerouri atunci când aveți un singur număr peste un anumit număr.

📝Ca un exercițiu rapid, urmați procedura de mai sus pentru a construi triunghiul lui Pascal pentru n = 6 și n = 7.

În continuare, să trecem la scrierea unui cod. Puteți alege să rulați fragmentele de cod pe IDE-ul Python al tipstrick.ro direct din browser – pe măsură ce vă parcurgeți tutorialul.

Funcția Python pentru a imprima triunghiul lui Pascal

În această secțiune, să scriem o funcție Python pentru a tipări triunghiul lui Pascal pentru orice număr dat de rânduri.

Există două întrebări cheie de luat în considerare:

  • Cum se exprimă intrările din triunghiul lui Pascal?
  • Cum să imprimați triunghiul lui Pascal cu spațierea și formatarea corespunzătoare?

Să le răspundem acum.

#1. Care este expresia pentru fiecare intrare din triunghiul lui Pascal?

Se întâmplă că intrările din triunghiul lui Pascal pot fi obținute folosind formula pentru nCr. Dacă vă amintiți din matematica de la școală, nCr indică numărul de moduri în care puteți alege r elemente dintr-un set de n articole.

Formula pentru nCr este dată mai jos:

Formula nCr (Imaginea autorului)

Acum să continuăm să exprimăm intrările din triunghiul lui Pascal folosind formula nCr.

Triunghiul lui Pascal folosind nCr (Imaginea autorului)

Am găsit acum o modalitate de a exprima intrările din matrice.

#2. Cum se reglează spațierea la imprimarea modelului?

În triunghiul lui Pascal cu numRows, rândul #1 are o singură intrare, rândul #2 are două intrări și așa mai departe. Pentru a imprima modelul ca triunghi, veți avea nevoie de numRows – i spații în rândul #i. Și puteți utiliza funcția range din Python împreună cu bucla for pentru a face acest lucru.

Deoarece funcția de interval exclude punctul final în mod implicit, asigurați-vă că adăugați + 1 pentru a obține numărul necesar de spații de început.

Acum că ați învățat cum să reprezentați intrările și, de asemenea, să ajustați spațiul în timp ce tipăriți triunghiul lui Pascal, haideți să definim funcția pascal_tri.

Analizarea definiției funcției

Deci, ce vrei să facă funcția pascal_tri?

  • Funcția pascal_tri ar trebui să accepte numărul de rânduri (numRows) ca argument.
  • Ar trebui să imprime triunghiul lui Pascal cu numRows.

Pentru a calcula factorialul, să folosim funcția factorială din modulul de matematică încorporat al lui Python.

▶️ Rulați următoarea celulă de cod pentru a importa factorial și utilizați-l în modulul curent.

from math import factorial

Fragmentul de cod de mai jos conține definiția funcției.

def pascal_tri(numRows):
  '''Print Pascal's triangle with numRows.'''
  for i in range(numRows):
    # loop to get leading spaces
	  for j in range(numRows-i+1):
		  print(end=" ")
    
    # loop to get elements of row i
	  for j in range(i+1):
		  # nCr = n!/((n-r)!*r!)
		  print(factorial(i)//(factorial(j)*factorial(i-j)), end=" ")

	 # print each row in a new line
	  print("n")

Funcția funcționează după cum urmează:

  • Funcția pascal_tri are un parametru necesar numRows: numărul de rânduri.
  • Există numRows rânduri în total. Pentru fiecare rând i, adăugăm numRows – i spații de început înainte de prima intrare din rând.
  • Apoi folosim formula nCr pentru a calcula intrările individuale. Pentru rândul i, intrările sunt iCj unde j = {0,1,2,..,i}.
  • Observați că folosim // care efectuează împărțirea întregilor, deoarece ne-am dori ca intrările să fie numere întregi.
  • După ce ați calculat toate intrările într-un rând, tipăriți următorul rând într-o nouă linie.

🔗 După cum am adăugat un docstring, puteți utiliza funcția de ajutor încorporată din Python sau atributul __doc__ pentru a accesa șirul document al funcției. Fragmentul de cod de mai jos arată cum se face.

help(pascal_tri)

# Output
Help on function pascal_tri in module __main__:

pascal_tri(numRows)
    Print Pascal's triangle with numRows.

pascal_tri.__doc__

# Output
Print Pascal's triangle with numRows.

Acum să mergem mai departe și să apelăm funcția cu numărul de rânduri ca argument.

pascal_tri(3)

# Output
     1
    1 1
   1 2 1

Primele 3 rânduri ale triunghiului lui Pascal sunt tipărite, așa cum era de așteptat.

Imprimați triunghiul lui Pascal folosind recursiunea

În secțiunea anterioară, am identificat expresia matematică a fiecărei intrări din Triunghiul Pascal. Cu toate acestea, nu am utilizat relația dintre intrări în două rânduri consecutive.

De fapt, am folosit rândul anterior pentru a calcula intrările din rândul următor. Nu putem folosi acest lucru și venim cu o implementare recursivă a funcției pascal_tri?

Da, hai să facem asta!

Într-o implementare recursivă, o funcție se autoapelează în mod repetat până când este îndeplinit cazul de bază. În construcția triunghiului lui Pascal, începem cu primul rând cu o intrare 1 și apoi construim rândurile următoare.

Deci, apelul funcției la pascal_tri(numRows) la rândul său apelează pascal_tri(numRows-1) și așa mai departe, până când este atins cazul de bază pascal_tri(1).

Luați în considerare exemplul în care trebuie să imprimați primele 3 rânduri ale triunghiului lui Pascal. Următoarea imagine explică modul în care apelurile recursive sunt împinse în stivă. Și cum apelurile funcției recursive returnează rândurile triunghiului lui Pascal.

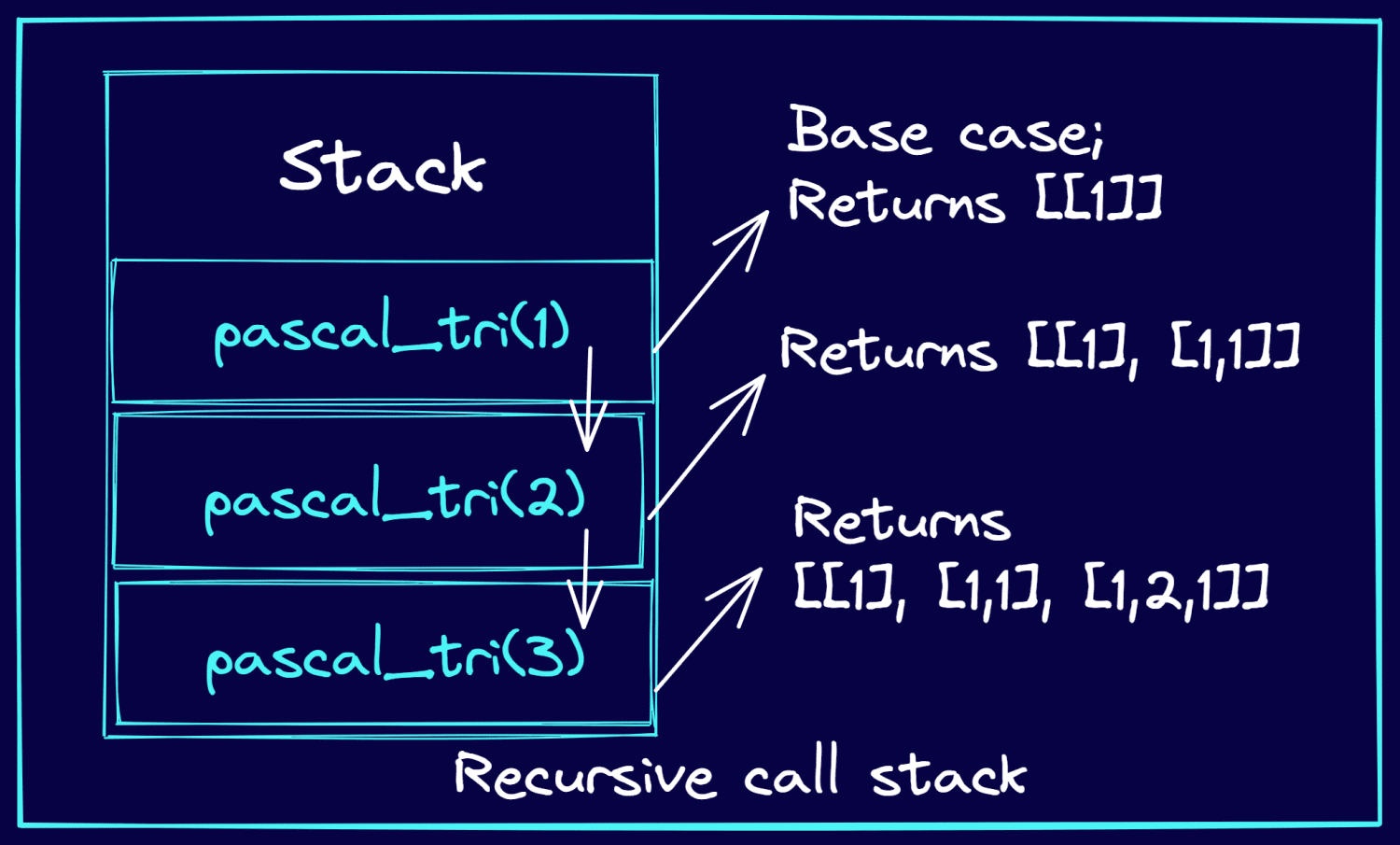Stivă de apeluri în timpul apelurilor recursive (Imaginea autorului)

▶️ Rulați fragmentul de cod de mai jos pentru a genera în mod recursiv rândurile triunghiului lui Pascal.

def pascal_tri(numRows):
    '''Print Pascal's triangle with numRows.'''
    if numRows == 1:
        return [[1]] # base case is reached!
    else:
        res_arr = pascal_tri(numRows-1) # recursive call to pascal_tri
        # use previous row to calculate current row 
        cur_row = [1] # every row starts with 1
        prev_row = res_arr[-1] 
        for i in range(len(prev_row)-1):
            # sum of 2 entries directly above
            cur_row.append(prev_row[i] + prev_row[i+1]) 
        cur_row += [1] # every row ends with 1
        res_arr.append(cur_row)
        return res_arr

Iată câteva puncte de care merită luate în considerare:

  • Am folosit o listă imbricată ca structură de date, unde fiecare rând din triunghiul lui Pascal este o listă în sine, astfel: [[row 1], [row 2],…,[row n]].
  • Apelul funcției pascal_tri(numRows) declanșează o serie de apeluri recursive cu numRows – 1, numRows – 2 până la 1 ca argumente. Aceste apeluri sunt împinse într-o stivă.
  • Când numRows == 1, am ajuns la cazul de bază, iar funcția revine [[1]].
  • Acum, lista returnată este utilizată de funcțiile ulterioare din stiva de apeluri – pentru a calcula următorul rând.
  • Dacă cur_row este rândul curent, cur_row[i] = rând_anterior[i] + prev_row[i+1]— suma a 2 elemente direct deasupra indicelui curent.

Deoarece matricea returnată este o listă imbricată (listă de liste), trebuie să ajustăm spațierea și să tipărim intrările, așa cum se arată în celula de cod de mai jos.

tri_array = pascal_tri(5)

for i,row in enumerate(tri_array):
  for j in range(len(tri_array) - i + 1):
    print(end=" ") # leading spaces
  for j in row:
    print(j, end=" ") # print entries
  print("n")  # print new line

Ieșirea este corectă, așa cum se vede mai jos!

# Output

       1

      1 1

     1 2 1

    1 3 3 1

   1 4 6 4 1

Funcția Python pentru a imprima triunghiul lui Pascal pentru numRows ≤ 5

Ambele metode pe care le-ați învățat vor funcționa pentru a tipări triunghiul lui Pascal pentru un număr arbitrar de rânduri numRows.

Cu toate acestea, există momente când trebuie să imprimați triunghiul lui Pascal pentru un număr mai mic de rânduri. Și când numărul de rânduri pe care trebuie să le imprimați este de cel mult 5, puteți utiliza o tehnică simplă.

Parcurgeți figura de mai jos. Și observați cum puterile lui 11 sunt identice cu intrările din triunghiul lui Pascal. De asemenea, observați că aceasta funcționează numai până la a 4-a putere a lui 11. Adică, 11 ridicat la puterile {0, 1, 2, 3, 4} oferă intrările din rândurile de la 1 la 5 ale triunghiului lui Pascal.

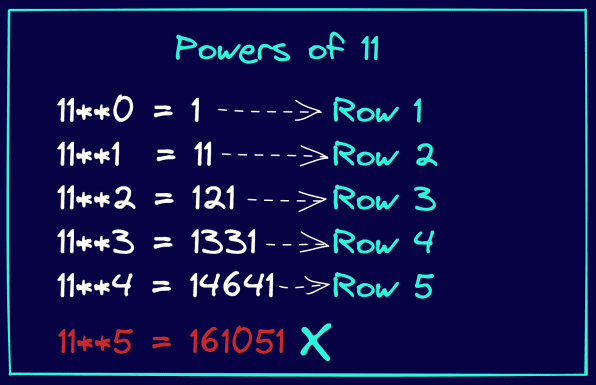
Să rescriem definiția funcției, așa cum se arată mai jos:

def pascal_tri(numRows):
  '''Print Pascal's triangle with numRows.'''
  for i in range(numRows):
    print(' '*(numRows-i), end='')
    # compute power of 11
    print(' '.join(str(11**i)))

Iată cum funcționează funcția pascal_tri:

  • Ca și în exemplele anterioare, ajustăm distanța.
  • Și apoi, folosim operatorul de exponențiere al lui Python (**) pentru a calcula puterile lui 11.
  • Deoarece puterile lui 11 sunt în mod implicit numere întregi, convertiți-le într-un șir folosind str(). Acum aveți puterile lui 11 ca șiruri.
  • Șirurile din Python sunt iterabile, astfel încât să le puteți parcurge și să accesați câte un caracter.
  • Apoi, puteți utiliza metoda join() cu sintaxa: .join() pentru a uni elemente în folosind ca separator.
  • Aici, aveți nevoie de un singur spațiu între caractere, deci va fi „ „, este șir: puterea lui 11.

Să verificăm dacă funcția funcționează conform intenției.

pascal_tri(5)

# Output
     1
    1 1
   1 2 1
  1 3 3 1
 1 4 6 4 1

Ca un alt exemplu, apelați funcția pascal_tri cu 4 ca argument.

pascal_tri(4)

# Output
     1
    1 1
   1 2 1
  1 3 3 1

Sper că știți să înțelegeți cum puteți imprima cu ușurință triunghiul Pascal pentru numRows în intervalul de la 1 la 5.

Concluzie

Iată ce am învățat:

  • Cum se construiește triunghiul lui Pascal cu numărul dat de rânduri. Fiecare număr din fiecare rând este suma celor două numere aflate direct deasupra lui.
  • Scrieți o funcție Python folosind formula nCr = n!/(nr)!.r! pentru a calcula intrările triunghiului lui Pascal.
  • Apoi ați învățat o implementare recursivă a funcției.
  • În cele din urmă, ați învățat cea mai optimă metodă de a construi triunghiul lui Pascal pentru numRows până la 5 – folosind puterile lui 11.

Dacă doriți să creșteți nivelul abilităților Python, învățați să înmulțiți matrice, să verificați dacă un număr este prim și să rezolvați probleme cu operațiunile cu șir. Codare fericită!