Analiza statistică a ipotezelor reprezintă un instrument valoros pentru specialiștii din diverse domenii, atât în sectorul privat cât și în cel guvernamental, permițându-le să formuleze afirmații și ipoteze fundamentate cu privire la datele populației.
Dacă ați lucrat sau ați studiat datele populației, este foarte probabil să fi întâlnit această metodologie esențială, testarea ipotezelor.
Există o varietate de metode prin care se pot construi ipoteze, dar nu toate oferă același nivel de acuratețe.
Utilizarea datelor incerte poate fi riscantă pentru o organizație, mai ales dacă nu sunteți complet sigur de calitatea lor.
Testarea ipotezelor este o strategie eficientă pentru a crește precizia analizelor. Aceasta s-a dovedit a fi fundamentală în evaluarea datelor populației.
În acest material, vom analiza ce înseamnă testarea ipotezelor, modul său de funcționare, avantajele pe care le oferă, precum și exemple concrete de aplicare.
Să începem, așadar, fără alte introduceri!
Ce presupune testarea ipotezelor?
Testarea ipotezelor este o tehnică de inferență statistică folosită de analiști pentru a evalua dacă datele referitoare la o populație susțin în mod corespunzător o anumită ipoteză, permițând formularea de concluzii pe această bază.
Această metodă facilitează evaluarea ipotezelor și determinarea gradului în care acestea sunt susținute de datele disponibile.
Simplu spus, este un proces de testare bazat pe statistici inferențiale, care permite formularea unei concluzii cu privire la datele populației, utilizând informațiile dintr-un eșantion colectat.
De obicei, este dificil pentru analiști să determine caracteristicile sau parametrii unei populații complete. Testarea ipotezelor oferă însă posibilitatea de a face predicții și de a lua decizii informate, pe baza datelor din eșantion și a acurateței lor.
Forme de testare a ipotezelor
Testarea ipotezelor se realizează în diverse forme, printre care:
- Ipoteza nulă: presupune că datele eșantionului nu evidențiază o corelație semnificativă între variabilele studiate.
- Ipoteza alternativă: reprezintă teza centrală și se opune ipotezei nule, demonstrând existența unei legături între variabilele studiate în eșantionul de date.
- Ipoteza non-direcțională: este o formă de testare cu două capete, care sugerează că nu există o direcție precisă între variabile și că valoarea reală diferă de cea prevăzută.
- Ipoteza direcțională: descrie o relație specifică între variabile, unde o variabilă din eșantion influențează altele.
- Ipoteza statistică: ajută analiștii să determine dacă datele și valorile se potrivesc unei ipoteze, facilitând formularea de afirmații și predicții privind rezultatul unui parametru al populației.
În continuare, vom explora metodele de testare a ipotezelor.
Metode de testare a ipotezelor
Pentru a stabili veridicitatea unei ipoteze, este necesar ca un analist să acumuleze dovezi solide. Procesul de testare implică formularea unei ipoteze nule și a unei ipoteze alternative, înainte de începerea evaluării.
Testarea ipotezelor nu se limitează la o singură tehnică, ci include o gamă de metode pentru a evalua relevanța datelor eșantionului. Analistul trebuie să țină cont de date și de dimensiunea eșantionului, selectând metoda de testare care se potrivește cel mai bine situației.
Testul de normalitate
Este o metodă standard pentru a analiza distribuția regulată a datelor într-un eșantion. În timpul testului, se verifică dacă valorile sunt grupate în jurul mediei, fiind situate deasupra sau sub aceasta.
În acest test statistic, probabilitatea ca valorile să fie situate deasupra sau sub medie este egală, rezultând o curbă în formă de clopot, distribuită uniform pe ambele părți ale mediei.
Testul Z
Acest test se aplică când datele populației urmează o distribuție normală. Se folosește pentru a evalua dacă mediile a doi parametri populaționali sunt diferite, în condițiile în care se cunoaște varianța datelor.
În general, testul Z este potrivit pentru eșantioane cu peste treizeci de elemente. Teorema limită centrală sprijină utilizarea testului Z, afirmând că, odată cu creșterea dimensiunii eșantioanelor, acestea tind să aibă o distribuție normală.
Testul T
Testul T este utilizat când dimensiunea eșantionului este redusă, având în mod obișnuit o distribuție limitată. Se aplică frecvent atunci când eșantioanele au mai puțin de 30 de elemente, iar abaterea standard a parametrului nu este cunoscută.
Scopul testului T este de a calcula intervalele de încredere pentru datele unei anumite populații.
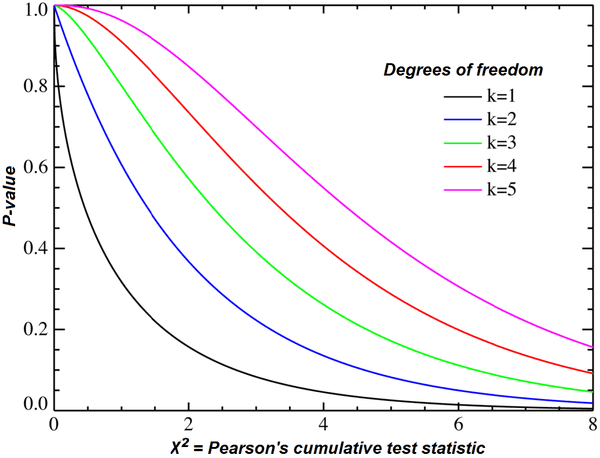
Testul Chi-Pătrat
Testul chi-pătrat este utilizat frecvent pentru a evalua adecvarea și integritatea unei distribuții de date.
 Sursa: wikipedia.org
Sursa: wikipedia.org
Acest test este ideal pentru compararea varianței unei populații cu o valoare ipotetică sau cunoscută. Există diverse variante ale testului Chi-Pătrat, dintre care cele mai comune sunt testele pentru varianță și independență.
Testul ANOVA

ANOVA (Analysis of Variance) este o metodă statistică de comparare a seturilor de date din două sau mai multe eșantioane, evaluând variabilele dependente și independente. Deși similară cu testele Z și T, ANOVA este mai adaptabilă, permițând compararea simultană a mai multor medii.
Cum se desfășoară testarea ipotezelor?
Analiștii folosesc date aleatorii din eșantioane pentru analize, utilizând aceste date pentru a testa ipoteza nulă și ipoteza alternativă.
Ipoteza nulă și cea alternativă sunt reciproc exclusive, astfel încât, doar una dintre ele poate fi confirmată ca adevărată în urma testării.
Există, totuși, cazuri în care, deși ipoteza nulă este respinsă, ipoteza alternativă nu este neapărat confirmată ca adevărată.
 Sursa: Analytics Steps
Sursa: Analytics Steps
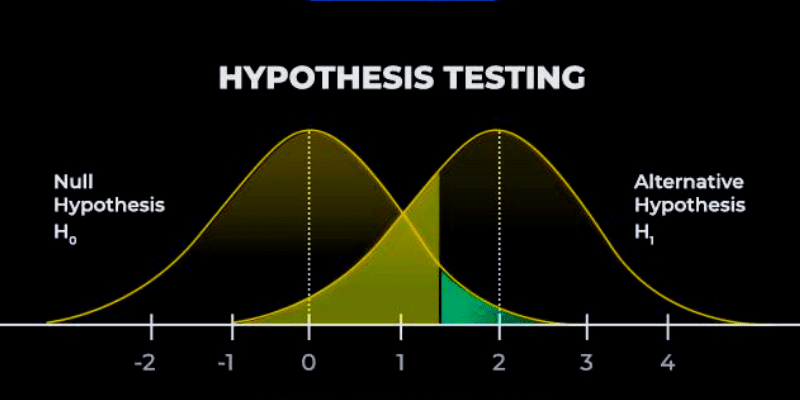
Valoarea p: Această valoare reprezintă probabilitatea obținerii unui rezultat la fel de extrem sau mai extrem decât cel observat, presupunând că ipoteza nulă este corectă. Valoarea p este comparată cu nivelul de semnificație (alfa) pentru a decide respingerea sau menținerea ipotezei nule.
Nivelul de semnificație indică riscul acceptabil de a respinge ipoteza nulă, deși este adevărată. Este esențial să se înțeleagă că testarea ipotezelor poate conduce la două tipuri de erori:
- Eroarea de tip 1: apare când ipoteza nulă este respinsă, deși este adevărată.
- Eroarea de tip 2: apare când ipoteza nulă este acceptată, deși este falsă.
Toate valorile care determină respingerea ipotezei nule sunt incluse în regiunea critică, separată de restul valorilor printr-o valoare critică.
Pașii testării ipotezelor
 Sursa: Mediu
Sursa: Mediu
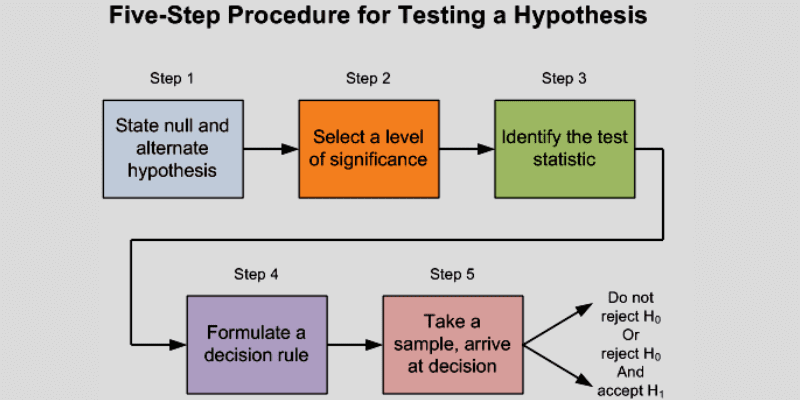
Testarea ipotezelor se desfășoară în patru etape principale:
- Definirea ipotezelor: Analistul trebuie să formuleze o ipoteză nulă și una alternativă, astfel încât doar una dintre ele să fie corectă. De exemplu, ipoteza nulă ar putea afirma că nu există o diferență în IMC mediu, în timp ce ipoteza alternativă ar sugera existența unei diferențe semnificative.
- Planificarea: Această etapă implică elaborarea unui plan de analiză pentru datele eșantionului, inclusiv modalitățile de colectare a datelor și de verificare a corespunderii lor cu scopul testului.
- Analiza datelor eșantionului: Presupune o evaluare minuțioasă a datelor, pentru a evita redundanțele. Trebuie verificate independența eșantioanelor și dimensiunea adecvată a acestora.
- Calculul statisticilor testului: Se determină valorile statistice ale testului și valoarea p, presupunând că ipoteza nulă este adevărată.
- Evaluarea rezultatului: Se decide respingerea sau acceptarea ipotezei nule, pe baza datelor eșantionului și a valorii p.
În continuare, vom examina avantajele testării ipotezelor.
Beneficiile testării ipotezelor
Avantajele testării ipotezelor sunt:
- Permite evaluarea riguroasă a validității unei afirmații privind datele.
- Oferă un cadru sigur pentru analiza datelor eșantionului.
- Ajută la determinarea semnificației statistice a eșantionului.
- Îmbunătățește fiabilitatea și validitatea rezultatelor în procesul de testare.
De asemenea, facilitează extrapolarea datelor dintr-un eșantion la o populație mai largă.
Aplicații ale testării ipotezelor
Testarea ipotezelor este utilizată în diverse sectoare pentru a evalua corectitudinea datelor. Câteva exemple practice sunt:
#1. Studii clinice
Testarea ipotezelor este esențială în studiile clinice, ajutând specialiștii medicali să evalueze eficacitatea unor noi medicamente, tratamente sau proceduri.
De exemplu, un medic poate investiga dacă un tratament reduce nivelul de potasiu la pacienți, comparând nivelurile de potasiu înainte și după tratament.

Testarea ipotezelor implică compararea a două ipoteze: H0 (nivelul de potasiu rămâne constant) și Ha (nivelul de potasiu scade după tratament). În cazul în care valoarea p este sub nivelul de semnificație, medicul poate concluziona că tratamentul este eficient.
#2. Producție
În sectorul manufacturier, testarea ipotezelor ajută la evaluarea eficacității noilor metode sau tehnici.
De exemplu, o fabrică poate utiliza testarea ipotezelor pentru a determina dacă o nouă metodă reduce numărul de produse defecte. Dacă, de exemplu, numărul inițial de produse defecte este de 300 per lot,

se poate compara media produselor defecte înainte și după aplicarea noii metode. Ipoteza nulă ar fi că media produselor defecte rămâne constantă, iar ipoteza alternativă ar afirma că media se modifică. Dacă valoarea p este sub nivelul de semnificație, se poate concluziona că metoda a avut un impact.
#3. Agricultură
În agricultură, testarea ipotezelor se folosește pentru a evalua efectul îngrășămintelor sau pesticidelor asupra creșterii plantelor. De exemplu, biologii pot testa dacă o plantă crește mai mult de 15 inci după aplicarea unui nou îngrășământ.

O ipoteză nulă ar putea fi că îngrășământul nu influențează creșterea medie a plantei (U=15 inci), iar ipoteza alternativă ar sugera că îngrășământul duce la o creștere mai mare (U>15 inci). Dacă valoarea p este sub nivelul de semnificație, se poate confirma efectul pozitiv al îngrășământului.
Resurse pentru învățare
#1. Statistici: o introducere pas cu pas, de la Udemy

Udemy oferă un curs introductiv despre statistici, care include și testarea ipotezelor. Cursul folosește exemple și lecții de la un fost cercetător Google, oferind o înțelegere solidă a intervalelor de încredere, testelor de ipoteze și altor concepte cheie.
#2. Statistici esențiale pentru analiza datelor, de la Udemy
Acest curs Udemy prezintă statistici prin proiecte reale, activități practice, teste de ipoteze, distribuții de probabilitate și analize de regresie.
#3. Statistici pentru știința datelor și analiza de afaceri

Acest curs Udemy acoperă o gamă largă de concepte statistice, inclusiv testarea ipotezelor, și este util pentru cercetătorii de date și analiștii de afaceri, care doresc să aprofundeze atât statisticile descriptive cât și cele inferențiale, împreună cu analiza de regresie.
#4. Testarea ipotezelor de Jim Frost
Această carte oferă un ghid intuitiv pentru luarea deciziilor bazate pe date, explicând modul de funcționare a testelor de ipoteză, importanța lor, modul de utilizare a intervalelor de încredere, valorile p și nivelurile de semnificație.
#5. Testarea ipotezelor de Scott Hartshorn
Această carte se distinge prin exemplele sale vizuale, fiind ideală pentru începătorii care doresc o introducere rapidă în testarea ipotezelor, explicând semnificația și tipurile de statistici și modul în care acestea funcționează.
Concluzie
Testarea ipotezelor este un instrument important pentru a verifica ipotezele și a dezvolta date statistice bazate pe evaluări. Această metodă, aplicabilă în diverse sectoare, ajută la luarea deciziilor informate și precise.
Pentru cei interesați să devină analiști de afaceri, resursele de învățare prezentate anterior pot oferi o bază solidă.