Sortarea listelor de date este o operație fundamentală în dezvoltarea aplicațiilor software.
Aceasta joacă un rol crucial în prezentarea informațiilor și facilitarea căutărilor eficiente. Nu este surprinzător că un inginer software competent trebuie să cunoască tehnicile de sortare a array-urilor. Acest articol explorează câțiva dintre cei mai uzitați algoritmi de sortare pentru array-uri în JavaScript.
Ce înseamnă sortarea și de ce este importantă?
 Sursă: Unsplash
Sursă: Unsplash
Sortarea se referă la aranjarea sistematică a datelor într-o anumită ordine, fie aceasta crescătoare, fie descrescătoare. Sortarea array-urilor în JavaScript este esențială, deoarece permite o prezentare mai clară și mai logică a datelor.
De exemplu, un utilizator poate dori să vizualizeze fișierele ordonate după data modificării sau produsele grupate după preț. Sortarea este, de asemenea, crucială pentru implementarea căutării binare, care funcționează exclusiv pe date sortate.
Deși există metode și biblioteci care simplifică sortarea, este vital să înțelegeți mecanismele de sortare, în special pentru interviurile de codificare sau când este necesară scrierea codului la nivel scăzut.
Algoritmi de sortare a array-urilor în JavaScript
Sortarea cu Bule

Sortarea cu Bule este, probabil, cel mai ușor algoritm de sortare, atât de înțeles, cât și de implementat. Acesta parcurge array-ul în mod repetat. În fiecare iterație, comparăm elementele adiacente și le interschimbăm dacă sunt în ordinea greșită.
Efectuăm un număr de treceri egal cu numărul de elemente din array. La fiecare trecere, elementele de la capătul array-ului sunt sortate progresiv. Iată o schiță în pseudocod a algoritmului pentru sortarea numerelor în ordine crescătoare:
1. Fie n numărul de elemente din array 2. Repetă de n ori (folosind i ca contor): a. Parcurge array-ul de la al doilea element până la al (n - i)-lea element b. Dacă elementul anterior este mai mare decât elementul curent, inversează-le.
Traducând în JavaScript, codul arată astfel:
function sort(arr) {
const n = arr.length;
for (let i = 0; i < n; i++) {
for (let j = 1; j < n - i; j++) {
if (arr[j - 1] > arr[j]) {
const temp = arr[j - 1];
arr[j - 1] = arr[j];
arr[j] = temp;
}
}
}
return arr;
}
Pentru a înțelege mai clar funcționarea algoritmului, este util să adăugați instrucțiuni `console.log` în ambele bucle, pentru a observa cum se modifică array-ul la fiecare pas.
Mai jos este o versiune modificată a funcției de sortare, care include `console.log`, alături de un exemplu de array nesortat pe care îl sortăm folosind funcția.
function sort(arr) {
const n = arr.length;
for (let i = 0; i < n; i++) {
console.log(`Pass: ${i}`);
for (let j = 1; j < n - i; j++) {
if (arr[j - 1] > arr[j]) {
const temp = arr[j - 1];
arr[j - 1] = arr[j];
arr[j] = temp;
}
console.log(arr);
}
}
return arr;
}
const array = [9, 2, 7, 4, 1];
sort(array);
console.log(array);
Rezultatul execuției codului de mai sus va fi:

Sortarea cu bule are o complexitate temporală de ordinul O(n^2), deoarece efectuează `n` treceri, parcurgând array-ul de fiecare dată. Din acest motiv, nu este foarte eficientă pentru seturi mari de date. Cu toate acestea, are o complexitate spațială de O(1), deoarece modifică array-ul direct în memorie.
Sortarea prin Inserție

Sortarea prin inserție este un algoritm des folosit pentru sortarea array-urilor în JavaScript. Pentru a înțelege mai bine funcționarea, vom considera cazul sortării în ordine crescătoare. Algoritmul alege un element pe care îl numim „num”. Apoi, deplasează „num” spre stânga, atâta timp cât valorile din stânga sa sunt mai mari. Această procedură se aplică de la al doilea element până la capătul array-ului, rezultând un array sortat. Iată pseudocodul:
1. Fie n numărul de elemente din array
2. Repetă i de la 1 la n-1 (începând cu al doilea element):
a. Setează currentElement la array[i]
b. Setează j la i-1
c. Cât timp j >= 0 și array[j] > currentElement:
i. Deplasează array[j] la array[j+1]
ii. Decrementează j cu 1
d. Setează array[j+1] la currentElement
Implementarea în JavaScript a pseudocodului este următoarea:
function insertionSort(array) {
const n = array.length;
for (let i = 1; i < n; i++) {
const currentElement = array[i];
let j = i - 1;
while (j >= 0 && array[j] > currentElement) {
array[j + 1] = array[j];
j -= 1;
}
array[j + 1] = currentElement;
}
return array;
}
Similar cu Sortarea cu bule, adăugarea instrucțiunilor `console.log` permite vizualizarea algoritmului în acțiune. Fragmentul de cod de mai jos demonstrează funcționarea Sortării prin inserție:
function sort(array) {
const n = array.length;
for (let i = 1; i < n; i++) {
const currentElement = array[i];
let j = i - 1;
console.log("Placing element:", currentElement);
while (j >= 0 && array[j] > currentElement) {
array[j + 1] = array[j];
j -= 1;
}
array[j + 1] = currentElement;
console.log("Placed it at position:", j + 1);
console.log(array);
}
return array;
}
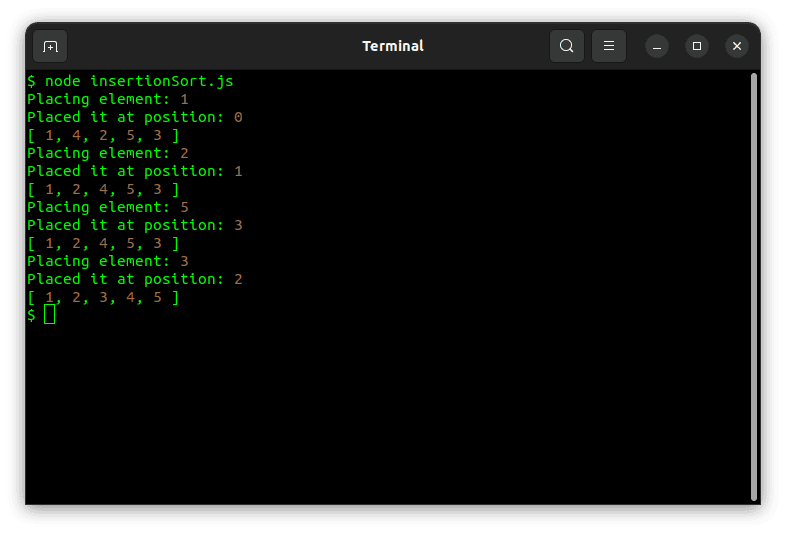
const array = [4, 1, 2, 5, 3];
sort(array);
Rularea fragmentului de mai sus va afișa:
Sortarea prin Interclasare (Merge Sort)

În timp ce Sortarea prin inserție și Sortarea cu bule au o complexitate temporală pătratică, Sortarea prin interclasare are o complexitate cvasi-liniară, adică O(n * log(n)).
Aceasta utilizează strategia „divide et impera”. Array-ul este împărțit în mod repetat în array-uri mai mici, fiecare conținând un singur element. După împărțire, array-urile sunt combinate în ordine.
Împărțirea este un proces recursiv, care permite ulterior reconstruirea array-ului.
La combinarea array-urilor, sub-array-urile sunt interclasate în ordine. Interclasarea se realizează similar cu interclasarea a două array-uri deja sortate. Iată pseudocodul:
1. Dacă lungimea array-ului este 1 sau mai mică, returnează array-ul (cazul de bază)
2. Găsește indicele de mijloc:
a. Setează mid la partea întreagă a (lungimea array-ului / 2)
3. Împarte array-ul în două sub-array-uri:
a. Creează leftArray și copiază prima jumătate a array-ului în el (de la indicele 0 la mid)
b. Creează rightArray și copiază a doua jumătate a array-ului în el (de la indicele mid+1 la sfârșit)
4. Apeleză recursiv MergeSort pe leftArray
5. Apeleză recursiv MergeSort pe rightArray
6. Interclasează cele două sub-array-uri sortate:
a. Creează un resultArray gol
b. Cât timp atât leftArray cât și rightArray nu sunt goale:
i. Dacă primul element din leftArray este mai mic sau egal cu primul element din rightArray, adaugă-l la resultArray
ii. Altfel, adaugă primul element din rightArray la resultArray
c. Adaugă elementele rămase din leftArray la resultArray (dacă există)
d. Adaugă elementele rămase din rightArray la resultArray (dacă există)
7. Returnează resultArray
Implementarea în JavaScript a acestui algoritm este:
function sort(array) {
// Base case in which we stop subdividing the array
if (array.length == 1) {
return array;
}
// Finding the middle point of the array
const m = Math.round(array.length / 2);
// Divide the array into two halves
const leftUnsorted = array.slice(0, m);
const rightUnsorted = array.slice(m);
// Recursively call merge sort
const leftSorted = sort(leftUnsorted);
const rightSorted = sort(rightUnsorted);
// Return a merged sorted array
return merge(leftSorted, rightSorted);
}
function merge(left, right) {
// Merge two sorted lists
let result = [];
let leftIndex = 0;
let rightIndex = 0;
while (leftIndex < left.length && rightIndex < right.length) {
if (left[leftIndex] < right[rightIndex]) {
result.push(left[leftIndex]);
leftIndex += 1;
} else {
result.push(right[rightIndex]);
rightIndex += 1;
}
}
return result.concat(left.slice(leftIndex), right.slice(rightIndex));
}
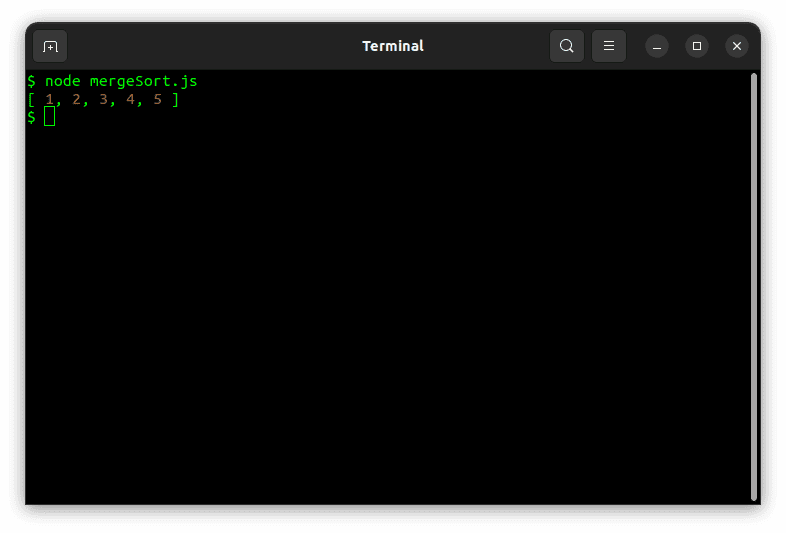
Rularea codului cu un array exemplu, va funcționa corect.
Sortarea Rapidă (Quick Sort)

Similar cu Sortarea prin interclasare, Sortarea rapidă se bazează pe strategia „divide et impera”. Algoritmul alege un element „pivot”. Apoi, deplasează toate elementele mai mari decât pivotul spre dreapta și cele mai mici spre stânga. În urma acestui proces, pivotul este poziționat corect.
Pentru a muta elementele, algoritmul începe prin a muta pivotul la capătul array-ului.
După mutarea pivotului, folosim un indicator pentru a parcurge array-ul de la stânga, căutând primul număr mai mare decât pivotul. În paralel, folosim un alt indicator care parcurge array-ul de la dreapta, căutând primul număr mai mic decât pivotul. Odată găsite ambele numere, le interschimbăm. Repetăm această procedură până când indicatorul din stânga depășește indicatorul din dreapta.
La final, interschimbăm cel mai mare dintre ultimele două numere cu pivotul. În acest moment, pivotul va fi poziționat corect; numerele mai mici vor fi la stânga, iar cele mai mari la dreapta.
Această procedură se repetă recursiv pentru sub-array-urile din stânga și din dreapta pivotului până când sub-array-urile conțin un singur element.
Iată pseudocodul Sortării rapide:
1. Dacă lessThanPointer este mai mic decât greaterThanPointer:
a. Alege un element pivot din array
b. Mută elementele astfel încât cele mai mici să fie la stânga și cele mai mari la dreapta:
c. Apelează recursiv Quicksort pe leftSubarray
d. Apelează recursiv Quicksort pe rightSubarray
Iar conversia sa în JavaScript:
function sort(array, low, high) {
if (low < high) {
// Choose the pivot index and partition the array
const pivotIndex = move(array, low, high);
// Recursively sort the subarrays to the left and right of the pivot
sort(array, low, pivotIndex - 1);
sort(array, pivotIndex + 1, high);
}
}
function move(array, low, high) {
// Select the pivot element (in this case, the last element)
const pivotElement = array[high];
// Initialize the index for the smaller element
let i = low - 1;
for (let j = low; j < high; j++) {
// If the current element is less than or equal to the pivot, swap it with the element at index i+1
if (array[j] <= pivotElement) {
i += 1;
const temp = array[i];
array[i] = array[j];
array[j] = temp;
}
}
// Swap the pivot element into its correct position
const temp = array[i];
array[i] = array[j];
array[j] = temp;
// Return the index of the pivot element
return i + 1;
}
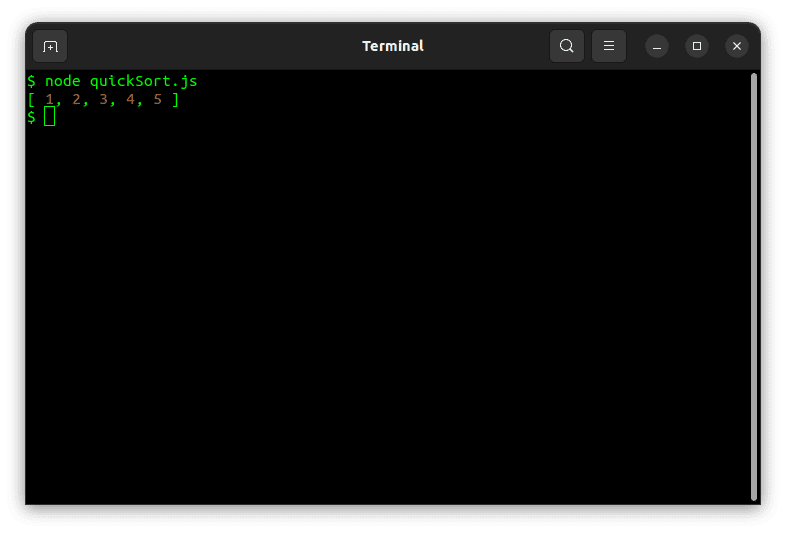
Sortarea unui array exemplu folosind Sortarea rapidă în Node.js va oferi următorul rezultat:
În cazul cel mai favorabil, Sortarea rapidă are o complexitate temporală cvasi-liniară. Utilizarea spațiului în Sortarea rapidă crește și ea logaritmic. Prin urmare, este relativ eficientă în comparație cu alți algoritmi de sortare a array-urilor în JavaScript.
Recomandări pentru interviurile de codificare
❇️ Practica este esențială. Ajută la înțelegerea diferiților algoritmi și, mai important, la dezvoltarea abilităților de rezolvare a problemelor și a gândirii computaționale. Platforme ca Leetcode și AlgoExpert oferă oportunități excelente de practică.
❇️ Încearcă mai întâi să rezolvi singur problema. Înainte de a căuta o soluție, încearcă să rezolvi problema pe cont propriu, deoarece aceasta te ajută să-ți dezvolți abilitățile de rezolvare.
❇️ Dacă o problemă durează prea mult, treci la soluție; poți învăța din ea. Majoritatea platformelor de învățare oferă soluții. Instrumente precum ChatGPT sau Google Bard sunt utile pentru explicarea conceptelor.
❇️ Nu începe imediat să scrii cod; analizează soluția și gândește-te la ea înainte. Pseudocodul este o modalitate eficientă de a-ți structura rapid ideile.
Concluzie
În acest articol, am explorat algoritmii de sortare cei mai uzitați. La început, învățarea acestora poate părea dificilă. De aceea, recomand combinarea informațiilor din diverse surse, în loc de a te baza exclusiv pe una singură. Mult succes la codare!
În continuare, verifică funcționalitatea `sorted` în Python.