Înțelegerea Eroarei Procentuale: Definiție, Calcul și Aplicații
Eroarea procentuală, într-un set de date, reprezintă diferența dintre valorile exacte și cele aproximative, raportată la valoarea inițială. Această diferență este exprimată ca procent, fiind, prin urmare, multiplicată cu 100.
Eroarea procentuală poate fi abordată fie ca o eroare absolută, fie ca o eroare relativă. Erorile pot apărea ca urmare a inexactităților instrumentelor, a erorilor de calcul, a greșelilor de măsurare sau a influențelor mediului înconjurător.
Calculul erorii procentuale ne permite să evaluăm cât de importante sunt greșelile noastre în cadrul unei analize. Valori procentuale mici indică o apropiere de valoarea inițială, în timp ce erori procentuale mari semnalează o discrepanță semnificativă între valoarea reală și cea estimată.
De exemplu, o eroare de 2% sugerează că aproximarea este foarte apropiată de valoarea originală, în timp ce o eroare de 56% arată o diferență substanțială între cele două valori.
Erorile sunt frecvente în procesul de măsurare, datorită posibilității de tremur al mâinilor, a defectelor instrumentelor, a inexactității materialelor etc.
Cum se Calculează Eroarea Procentuală
Pentru a calcula eroarea procentuală, este nevoie de două valori: valoarea exactă și valoarea aproximativă. Diferența dintre aceste valori se împarte la valoarea exactă, iar rezultatul se înmulțește cu 100. Această operațiune transformă eroarea relativă în eroare procentuală.
Formula de calcul este următoarea:
Eroare procentuală = [(Valoare Reală – Valoare Estimată) / Valoare Estimată] × 100
Componentele Formulei
Valoarea Reală: Aceasta reprezintă valoarea numerică ideală a unei măsurători, care ar fi trebuit înregistrată dacă nu ar fi existat erori. Este valoarea ideală, pe care încercăm să o aproximăm.
Valoarea Estimată: Aceasta este valoarea obținută în urma unei măsurători sau a unui experiment. De obicei, diferă de valoarea reală din cauza erorilor de instrument, a erorilor umane sau a factorilor de mediu.
Exemple Practice
Exemplul 1
Un elev măsoară suprafața unui triunghi și obține 462 cm². Valoarea reală a suprafeței este de 465 cm². Să calculăm eroarea procentuală.
Rezolvare:
Suprafața măsurată: 462 cm²
Suprafața reală: 465 cm²
Calcul:
Diferența: 465 – 462 = 3
Eroarea: 3
Eroarea împărțită la valoarea reală: 3 / 465 = 0.00645
Eroarea procentuală: 0.00645 x 100 = 0.64%
Așadar, eroarea procentuală este de 0.64%.
Exemplul 2
Pentru o petrecere, se așteaptă 20 de invitați, dar vin doar 18. Să determinăm eroarea procentuală.
Rezolvare:
Numărul estimat de invitați: 20
Numărul real de invitați: 18
Calcul:
Diferența: 20 – 18 = 2
Eroarea: 2
Eroarea împărțită la valoarea estimată: 2 / 20 = 0.1
Eroarea procentuală: 0.1 x 100 = 10%
Eroarea procentuală în estimarea numărului de invitați este de 10%.
Exemplul 3
Într-un experiment, se măsoară punctul de fierbere al apei, rezultând 102°C, în timp ce punctul real este de 100°C.
Rezolvare:
Punctul de fierbere real: 100°C
Punctul de fierbere măsurat: 102°C
Calcul:
Diferența: 102 – 100 = 2°C (Eroarea procentuală este întotdeauna pozitivă).
Eroarea: 2
Eroarea împărțită la valoarea reală: 2 / 100 = 0.02
Eroarea procentuală: 0.02 x 100 = 2%
Așadar, eroarea procentuală este de 2%.
Importanța Eroarei Procentuale în Situații Reale
- Ajută la evaluarea corectitudinii unei sarcini finalizate, evidențiind eventualele erori.
- Este esențială în laboratoare și în industrii unde chiar și cele mai mici erori pot avea consecințe majore.
- Este importantă în cadrul comenzilor mari, unde nu se acceptă abateri de la specificații.
- Este un instrument critic în laboratoarele științifice.
Eroarea Procentuală vs. Eroarea Absolută
Eroarea Absolută reprezintă diferența directă între valorile reale și cele estimate, păstrând unitatea de măsură a valorii inițiale.
Exemplu: Dacă dorești să cumperi 2 kg de mango, dar vânzătorul măsoară 1,98 kg, eroarea absolută este de 2 – 1,98 = 0,02 kg.
Eroarea Procentuală se calculează împărțind eroarea absolută la valoarea inițială și înmulțind cu 100, fiind o cantitate adimensională.
Exemplu: În exemplul de mai sus, eroarea procentuală este (0,02 / 2) x 100 = 1%.
Eroarea Procentuală vs. Eroarea Relativă
Eroarea Relativă se obține prin împărțirea erorii absolute la valoarea reală, exprimând eroarea ca o fracție a valorii inițiale.
Exemplu: Dacă prognoza meteo indică 38°C, dar temperatura reală este de 42°C, diferența este 4°C. Eroarea relativă este 4 / 38 = 0.1052.
Eroarea Procentuală este eroarea relativă înmulțită cu 100, exprimând eroarea ca procent.
Exemplu: În exemplul de mai sus, eroarea procentuală este 0.1052 x 100 = 10.52%.
Calculul erorii procentuale, relative sau absolute poate fi simplificat prin utilizarea calculatoarelor online.
Instrumente de Calcul al Erorilor
#1. Calculator Soup
Calculator Soup vă ajută să calculați eroarea procentuală dintre valoarea experimentală și cea reală. Introduceți valorile și așteptați rezultatele. Calculator Soup oferă rezultate precise rapid.
#2. Calculator.net
Calculator.net permite introducerea valorilor reale și estimate, simplificând procesul de calcul, mai ales în cazul volumelor mari de date.
Erorile procentuale sunt inevitabile, dar pot fi minimizate, chiar dacă este imposibil să atingem o valoare de zero.
#3. Calculatoare Bune
Multe calculatoare online sunt disponibile, iar Calculatoare Bune este un instrument util. Introduceți valorile și obțineți instantaneu rezultatele.
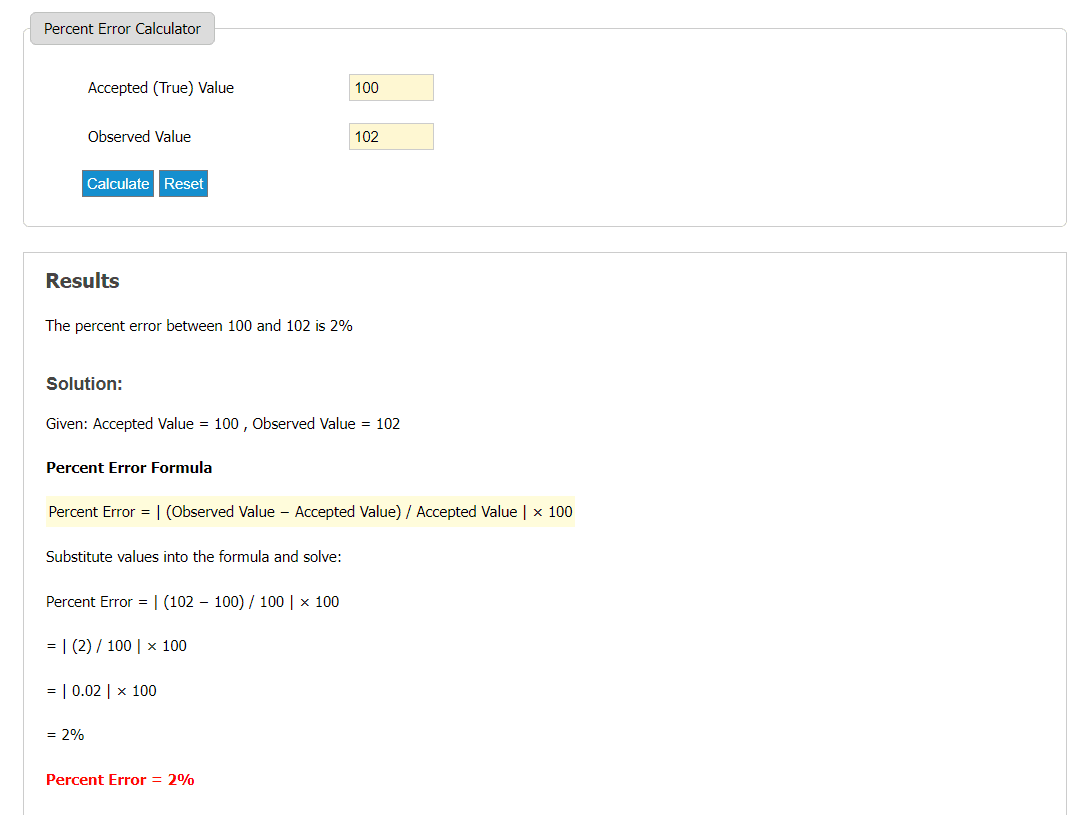
Un calculator online este ideal pentru calculul erorii procentuale când avem multe date de analizat, dar timpul este limitat.
Concluzie
Erorile de calcul pot afecta calitatea unui proiect sau a unei cercetări. Calculatoarele online pentru erori procentuale sunt instrumente utile pentru a spori eficiența și a reduce erorile umane.
Pentru cei interesați de finanțe, există calculatoare de procentaj de profit disponibile.