În lumea programării, procesul de sortare a datelor este o operație fundamentală, frecvent întâlnită. Eficiența acestui proces depinde în mod crucial de algoritmul ales. O selecție inadecvată a algoritmului poate duce la o durată de execuție semnificativă, mai ales în cazul seturilor mari de date.
În acest articol, vom explora o varietate de algoritmi de sortare, analizând caracteristicile și implementările lor.
Vom oferi o prezentare detaliată a diferiților algoritmi de sortare, incluzând explicații pas cu pas pentru implementare. Vom folosi limbajul Python pentru a demonstra implementările, dar principiile de bază pot fi ușor adaptate la orice alt limbaj de programare. Esența constă în înțelegerea algoritmului, nu în sintaxa specifică a unui limbaj.
Vom prezenta algoritmii de la cei mai puțin eficienți, spre cei mai performanți. Nu vă faceți griji dacă unele concepte par inițial complicate; urmăriți explicațiile și experimentați cu implementările. Fiecare algoritm va fi analizat în detaliu.
Să analizăm în detaliu algoritmii de sortare.
Sortarea prin Inserție
Sortarea prin inserție este un algoritm de sortare simplu și intuitiv. Datorită ușurinței implementării, este adesea folosit ca prim exemplu în studiul algoritmilor de sortare. Cu toate acestea, nu este cea mai eficientă opțiune pentru seturi mari de date, având o performanță mai slabă în comparație cu alți algoritmi.
Acest algoritm menține două submulțimi: una sortată și una nesortată. La început, submulțimea sortată conține doar primul element al tabloului.
Algoritmul parcurge elementele din submulțimea nesortată și le inserează în poziția corectă în submulțimea sortată. Acest proces se repetă până când toate elementele sunt sortate.
Pentru o înțelegere mai clară, să analizăm pas cu pas ilustrațiile vizuale ale sortării prin inserție:
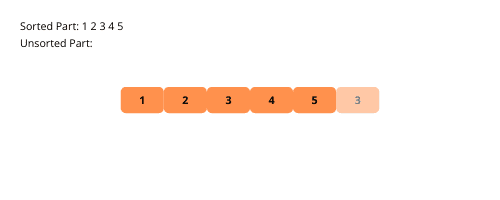
Iată pașii specifici pentru implementarea sortării prin inserție:
- Începem prin a inițializa un tablou cu valori arbitrare (numere întregi).
- Iterăm prin tablou, începând cu al doilea element.
- Salvez poziția curentă și valoarea elementului curent în variabile temporare.
- Inițializăm o buclă care continuă până când se ajunge la începutul tabloului sau se găsește un element mai mic decât cel curent.
- Mutăm elementul anterior în poziția actuală.
- Decremenăm poziția curentă.
- Inserăm valoarea elementului curent în poziția corectă, fie la începutul tabloului, fie după ce am întâlnit un element mai mic.
Complexitatea temporală a sortării prin inserție este O(n^2), iar complexitatea spațială este O(1).
Cu aceasta am sortat tabloul. Să executăm codul de mai jos. Pentru a rula codul, asigurați-vă că aveți Python instalat; în caz contrar, consultați un ghid de instalare. Alternativ, puteți folosi un compilator Python online.
def insertion_sort(arr, n):
for i in range(1, n):
# poziția curentă și elementul
current_position = i
current_element = arr[i]
# iterăm până când
# se ajunge la primul element sau
# elementul curent este mai mic decât elementul precedent
while current_position > 0 and current_element < arr[current_position - 1]:
# actualizarea elementului curent cu elementul precedent
arr[current_position] = arr[current_position - 1]
# trecerea la poziția anterioară
current_position -= 1
# actualizarea elementului poziției curente
arr[current_position] = current_element
if __name__ == '__main__':
# inițializarea tabloului
arr = [3, 4, 7, 8, 1, 9, 5, 2, 6]
insertion_sort(arr, 9)
# afișarea tabloului
print(str(arr))
Sortarea prin Selecție
Sortarea prin selecție este similară sortării prin inserție, dar diferă prin modul în care determină poziția corectă a elementelor. La fel ca sortarea prin inserție, sortarea prin selecție împarte tabloul în două submulțimi: una sortată și una nesortată.
La fiecare iterație, sortarea prin selecție caută elementul minim din submulțimea nesortată și îl plasează la sfârșitul submulțimii sortate.
Pentru o înțelegere mai bună, haideți să analizăm ilustrațiile sortării prin selecție:
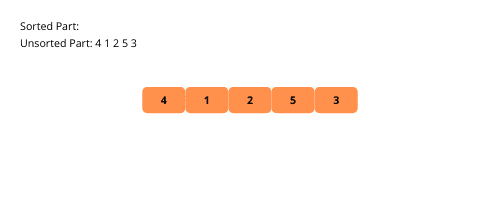
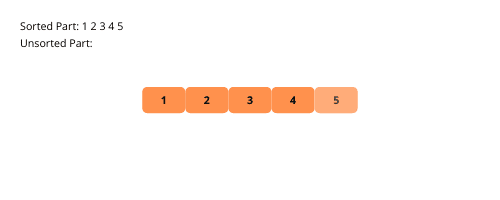
Iată pașii pentru implementarea sortării prin selecție:
- Inițializăm un tablou cu valori arbitrare (numere întregi).
- Iterăm prin tablou.
- Menținem indexul elementului minim.
- Iterăm de la elementul curent până la ultimul element.
- Verificăm dacă elementul curent este mai mic decât elementul minim.
- Dacă elementul curent este mai mic, actualizăm indexul minim.
- După ce am găsit elementul minim, schimbăm elementul curent cu elementul minim folosind indecșii.
Complexitatea temporală a sortării prin selecție este O(n^2), iar complexitatea spațială este O(1).
Încercați să implementați algoritmul; este destul de similar cu sortarea prin inserție. Puteți analiza codul de mai jos.
def selection_sort(arr, n):
for i in range(n):
# pentru a stoca indexul elementului minim
min_element_index = i
for j in range(i + 1, n):
# verificăm și înlocuim indexul elementului minim
if arr[j] < arr[min_element_index]:
min_element_index = j
# schimbăm elementul curent cu elementul minim
arr[i], arr[min_element_index] = arr[min_element_index], arr[i]
if __name__ == '__main__':
# inițializarea tabloului
arr = [3, 4, 7, 8, 1, 9, 5, 2, 6]
selection_sort(arr, 9)
# afișarea tabloului
print(str(arr))
Sortarea cu Bule
Sortarea cu bule este un algoritm simplu, dar nu foarte eficient. El compară elemente adiacente și le schimbă între ele în mod repetat până când întregul tablou este sortat.
Sortarea cu bule iterează prin tablou, mutând elementul curent către următoarea poziție până când acesta este mai mic decât elementul următor.
Ilustrațiile următoare ajută la vizualizarea procesului de sortare cu bule:
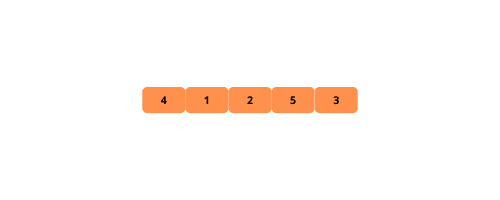
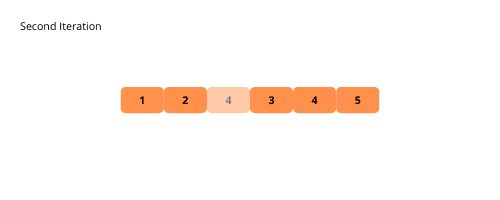
Iată pașii pentru implementarea sortării cu bule:
Complexitatea temporală a sortării cu bule este O(n^2), iar complexitatea spațială este O(1).
Probabil că puteți implementa cu ușurință sortarea cu bule. Să vedem codul:
def bubble_sort(arr, n):
for i in range(n):
# iterăm de la 0 la n-i-1, ultimele i elemente fiind deja sortate
for j in range(n - i - 1):
# verificăm elementul următor
if arr[j] > arr[j + 1]:
# schimbăm elementele adiacente
arr[j], arr[j + 1] = arr[j + 1], arr[j]
if __name__ == '__main__':
# inițializarea tabloului
arr = [3, 4, 7, 8, 1, 9, 5, 2, 6]
bubble_sort(arr, 9)
# afișarea tabloului
print(str(arr))
Sortarea prin Interclasare (Merge Sort)
Sortarea prin interclasare este un algoritm recursiv, mult mai eficient decât algoritmii prezentați anterior, în special pentru seturi mari de date. Algoritmul urmează strategia „divide și cucerește”.
Algoritmul împarte tabloul în două jumătăți, sortează fiecare jumătate separat și apoi combină cele două jumătăți sortate într-un singur tablou sortat.
Datorită naturii sale recursive, algoritmul împarte continuu tabloul până când se ajunge la cele mai simple subtablouri (tablouri cu un singur element) care sunt automat sortate.
Este timpul pentru o ilustrație. Să o analizăm:
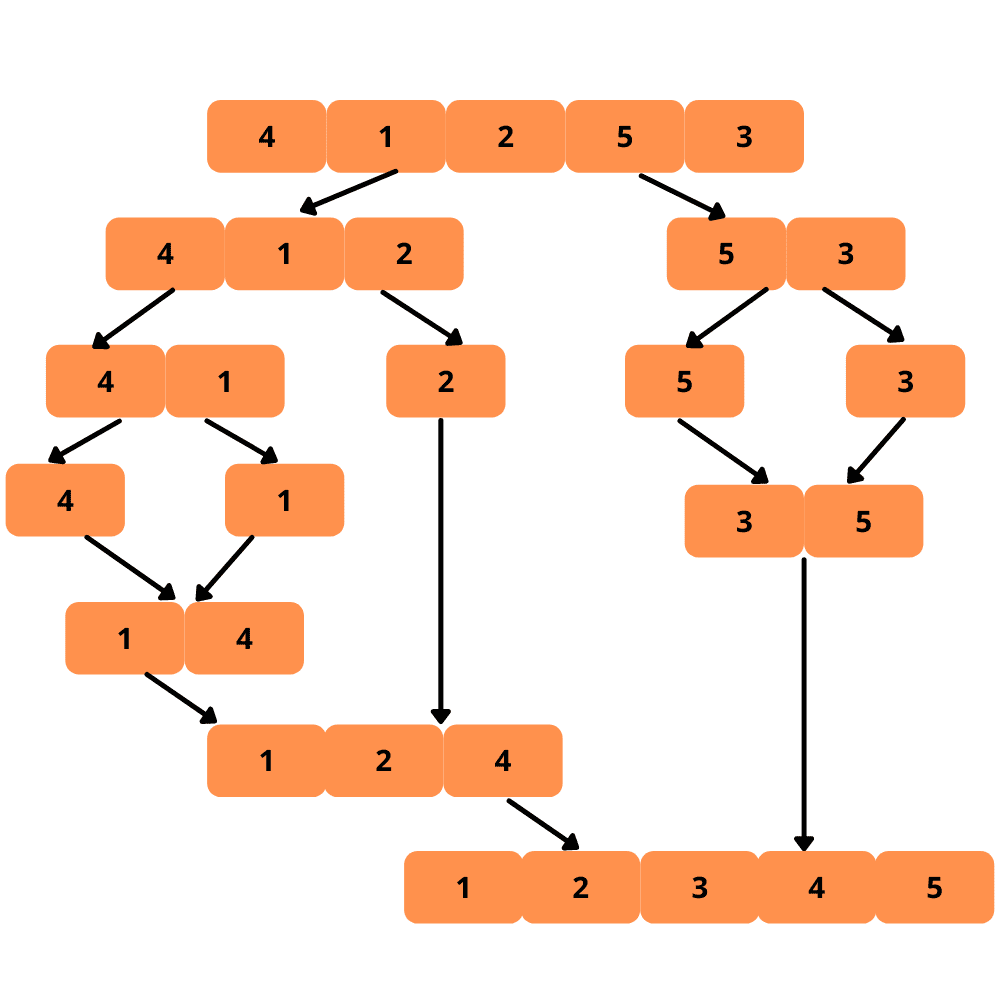
Să vedem pașii pentru implementarea sortării prin interclasare:
- Inițializăm un tablou cu valori arbitrare (numere întregi).
- Scriem o funcție numită `merge` pentru a îmbina două subtablouri sortate într-un singur tablou sortat. Aceasta primește ca argumente tabloul, indicii stânga, mijloc și dreapta.
- Calculăm lungimile celor două subtablouri.
- Copiem elementele din tablou în subtablourile corespunzătoare.
- Iterăm prin cele două subtablouri.
- Comparăm elementele celor două subtablouri.
- Plasăm elementul mai mic în tabloul principal.
- Adăugăm eventualele elemente rămase în subtablouri.
- Scriem o funcție numită `merge_sort` cu parametrii: tabloul și indicii stânga și dreapta.
- Dacă indexul din stânga este mai mare sau egal cu cel din dreapta, atunci ne oprim.
- Calculăm indicele mijlociu pentru a împărți tabloul în două jumătăți.
- Apelăm recursiv `merge_sort` pentru cele două jumătăți.
- După apelurile recursive, interclasăm tabloul folosind funcția `merge`.
Complexitatea temporală a sortării prin interclasare este O(n log n), iar complexitatea spațială este O(n) datorită tablourilor temporare.
Asta este tot pentru implementarea algoritmului de sortare prin interclasare. Verifică codul de mai jos:
def merge(arr, left_index, mid_index, right_index):
# tablourile stânga și dreapta
left_array = arr[left_index:mid_index+1]
right_array = arr[mid_index+1:right_index+1]
# obținem lungimile tablourilor stânga și dreapta
left_array_length = mid_index - left_index + 1
right_array_length = right_index - mid_index
# indici pentru interclasarea celor două tablouri
i = j = 0
# index pentru înlocuirea elementelor tabloului
k = left_index
# iterăm prin cele două subtablouri
while i < left_array_length and j < right_array_length:
# comparăm elementele din tablourile stânga și dreapta
if left_array[i] < right_array[j]:
arr[k] = left_array[i]
i += 1
else:
arr[k] = right_array[j]
j += 1
k += 1
# adăugăm elementele rămase din tablourile stânga și dreapta
while i < left_array_length:
arr[k] = left_array[i]
i += 1
k += 1
while j < right_array_length:
j += 1
k += 1
def merge_sort(arr, left_index, right_index):
# cazul de bază pentru funcția recursivă
if left_index >= right_index:
return
# găsim indicele mijlociu
mid_index = (left_index + right_index) // 2
# apeluri recursive
merge_sort(arr, left_index, mid_index)
merge_sort(arr, mid_index + 1, right_index)
# interclasăm cele două subtablouri
merge(arr, left_index, mid_index, right_index)
if __name__ == '__main__':
# inițializarea tabloului
arr = [3, 4, 7, 8, 1, 9, 5, 2, 6]
merge_sort(arr, 0, 8)
# afișarea tabloului
print(str(arr))
Concluzie
Există numeroși alți algoritmi de sortare, dar cei prezentați sunt printre cei mai frecvent utilizați. Sperăm că v-a plăcut această incursiune în lumea algoritmilor de sortare.
Următorul pas logic este explorarea algoritmilor de căutare.
Spor la programare! 🙂 👨💻