Implementări de algoritmi de căutare în Python

Implementarea unui mecanism de căutare reprezintă întotdeauna o provocare, dar nu una insurmontabilă.

În viața de zi cu zi, când căutăm ceva, nu ne ghidăm după un model anume. Ne îndreptăm instinctiv către locurile unde credem că ar putea fi acel lucru. De cele mai multe ori, nu urmăm un tipar predefinit.

Dar oare funcționează la fel și în lumea programării?

Răspunsul este nu! În programare, există tipare clare pentru a găsi elemente. În acest articol, vom explora câțiva algoritmi care folosesc diverse abordări pentru căutare.

În universul programării, se găsesc numeroși algoritmi de căutare. Vom analiza aici cei mai importanți și utilizați algoritmi, oferind o bază solidă pentru înțelegerea celorlalți.

În contextul acestui articol, căutarea se referă la procesul de a identifica un anumit element într-o structură de tip matrice.

Haideți să îi analizăm pe fiecare în parte.

Căutarea Liniară

Denumirea acestui algoritm, „căutare liniară,” sugerează metoda sa de operare. Algoritmul parcurge elementele matricei într-o manieră liniară, începând de la primul element și continuând până când găsește elementul căutat sau ajunge la finalul matricei. Odată ce elementul este identificat, algoritmul se oprește.

Pentru o înțelegere mai clară a acestui algoritm, vom folosi câteva ilustrații.

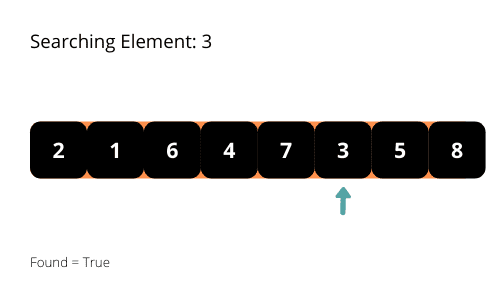
Observând modul în care algoritmul parcurge matricea, se poate deduce că, în cel mai defavorabil scenariu, timpul de execuție va fi de O(n). Atunci când analizăm algoritmii, este crucial să luăm în considerare complexitatea temporală în cel mai rău caz. Prin urmare, complexitatea temporală a căutării liniare este O(n).

Să analizăm acum implementarea acestui algoritm.

Implementarea Căutării Liniare

Acum că ați înțeles conceptul din spatele căutării liniare, este momentul să trecem la cod. Vom începe prin a descrie pașii necesari pentru implementare, apoi vă voi oferi codul sursă. Nu vă îngrijorați dacă nu reușiți să îl codificați de la început, codul complet va fi disponibil ulterior.

Iată pașii necesari pentru implementarea algoritmului de căutare liniară:

• Inițializați o matrice cu elemente (pot fi numere alese aleatoriu).
• Definiți o funcție, denumită de exemplu ‘cauta_element’, care primește ca argumente matricea, lungimea acesteia și elementul de căutat.
• În interiorul funcției ‘cauta_element(matrice, lungime, element)’:
  • Iterați prin matrice.
    • Verificați dacă elementul curent este egal cu cel căutat.
    • În caz afirmativ, returnați ‘Adevărat’.
  • Dacă iterația se încheie fără a găsi elementul, înseamnă că acesta nu se află în matrice, deci returnați ‘Fals’.
• În funcție de valoarea returnată de funcția ‘cauta_element’, afișați un mesaj adecvat.

Pe baza acestor pași, scrieți codul pentru a implementa căutarea liniară.

Ați reușit să implementați algoritmul? Sperăm că da. Dacă ați terminat, verificați codul de mai jos.

Dacă nu l-ați finalizat, nu vă faceți probleme, analizați codul de mai jos și veți înțelege cu ușurință implementarea. Este mai simplu decât pare.

def cauta_element(matrice, lungime, element):
    for i in range(lungime):
        if matrice[i] == element:
            return True
    return False


if __name__ == '__main__':
    matrice = [1, 2, 3, 4, 5, 6, 7, 8, 9, 10]
    lungime = 10
    element_cautat = 6

    if cauta_element(matrice, lungime, element_cautat):
        print(element_cautat, "a fost gasit")
    else:
        print(element_cautat, "nu a fost gasit")

Rulați programul mai întâi cu un element care este prezent în matrice, apoi repetați procesul cu un element care lipsește.

Complexitatea temporală a algoritmului de căutare liniară este O(n).

Putem reduce complexitatea temporală folosind un alt algoritm?

Da, putem. Să vedem cum.

Căutarea Binară

Algoritmul de căutare binară verifică întotdeauna elementul din mijlocul matricei. Acest algoritm este aplicabil doar pentru matricele sortate.

Algoritmul parcurge matricea, verificând elementul din mijloc. Dacă acesta este elementul căutat, algoritmul se oprește. Dacă elementul din mijloc este mai mic decât cel căutat, atunci algoritmul ignoră partea stângă a matricei, concentrându-se pe partea dreaptă. Dacă elementul din mijloc este mai mare, algoritmul ignoră partea dreaptă, concentrându-se pe partea stângă.

În fiecare iterație, algoritmul de căutare binară reduce zona de căutare, ceea ce înseamnă că verifică mai puține elemente decât algoritmul de căutare liniară.

Ilustrațiile ne pot ajuta să înțelegem mai bine acest algoritm. Să le analizăm.

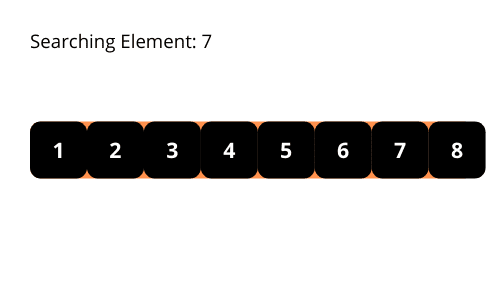
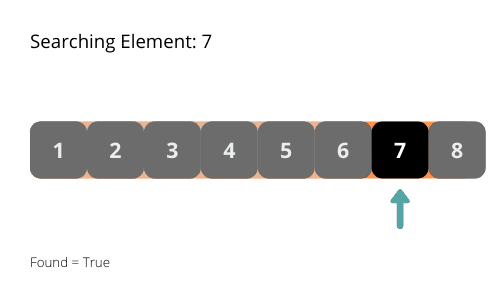
Complexitatea temporală a algoritmului de căutare binară este O(log n). În fiecare iterație, lungimea zonei de căutare se reduce la jumătate, scăzând exponențial.

Implementarea Căutării Binare

Vom descrie mai întâi pașii necesari pentru implementarea algoritmului de căutare binară, apoi vom analiza codul. Iată pașii pentru a realiza implementarea algoritmului:

• Inițializați matricea cu elemente sortate.
• Definiți o funcție, denumită de exemplu ‘cauta_element’, care primește ca argumente matricea sortată, lungimea matricei și elementul de căutat.
• În interiorul funcției ‘cauta_element(matrice_sortata, lungime, element)’:
  • Inițializați o variabilă ‘i’ care va servi ca indice de iterație.
  • Inițializați două variabile pentru a defini zona de căutare. Le vom denumi ‘inceput’ și ‘sfarsit’, indicând pozițiile limită ale zonei de căutare.
  • Iterați atâta timp cât ‘i’ este mai mic decât lungimea matricei.
    • Calculați indicele elementului din mijlocul zonei de căutare, folosind formula (inceput + sfarsit) // 2.
    • Verificați dacă elementul de la indicele mijloc este egal cu elementul căutat.
    • În caz afirmativ, returnați ‘Adevărat’.
    • Dacă elementul de la mijloc este mai mic decât cel căutat, atunci mutați indicele ‘inceput’ la mijloc + 1.
    • Dacă elementul de la mijloc este mai mare decât cel căutat, mutați indicele ‘sfarsit’ la mijloc – 1.
    • Incrementați indicele ‘i’.
  • Dacă iterația se încheie fără a găsi elementul căutat, înseamnă că acesta nu se află în matrice, deci returnați ‘Fals’.
• Afișați un mesaj adecvat în funcție de valoarea returnată de funcția ‘cauta_element’.

Încercați să scrieți codul, similar cu implementarea algoritmului de căutare liniară.

…

Ați reușit să scrieți codul?

Comparați-l cu codul de mai jos. Dacă nu ați reușit, nu vă faceți griji, analizați codul de mai jos și veți înțelege implementarea. Este mai simplu decât pare.

def cauta_element(matrice_sortata, lungime, element):
    i = 0
    start = 0
    end = lungime - 1

    while i < lungime:
        middle = (start + end) // 2
        if matrice_sortata[middle] == element:
            return True
        elif matrice_sortata[middle] < element:
            start = middle + 1
        else:
            end = middle - 1
        i += 1
    return False

if __name__ == '__main__':
    matrice = [1, 2, 3, 4, 5, 6, 7, 8, 9, 10]
    lungime = 10
    element_cautat = 9

    if cauta_element(matrice, lungime, element_cautat):
        print(element_cautat, "a fost gasit")
    else:
        print(element_cautat, "nu a fost gasit")

Testați codul cu diverse scenarii, în care elementul este prezent, respectiv absent din matrice.

Concluzie

Algoritmul de căutare binară este mult mai eficient decât cel de căutare liniară. Totuși, trebuie să sortăm matricea înainte de a folosi algoritmul de căutare binară, ceea ce nu este necesar în cazul căutării liniare. Sortarea necesită timp, dar folosirea unor algoritmi de sortare eficienți, în combinație cu algoritmul de căutare binară, poate duce la o soluție foarte rapidă.

Acum aveți o înțelegere solidă a unora dintre cei mai folosiți algoritmi de căutare din Python.

Pentru a aprofunda cunoștințele, ar trebui să explorați diversele programe de căutare self-hosted.

Spor la codare! 🙂 🧑‍💻