Analiza Big O: Un Ghid Detaliat
Analiza Big O reprezintă o metodă esențială pentru a evalua și clasifica eficiența algoritmilor. Această tehnică ne permite să identificăm algoritmii cei mai performanți și adaptabili la volume mari de date. Acest ghid detaliat îți oferă toate informațiile necesare despre notația Big O.
Ce este Analiza Big O?
Analiza Big O este o metodă de a evalua modul în care algoritmul se comportă pe măsură ce cantitatea de date de intrare crește. Întrebarea principală este cât de eficient este un algoritm în gestionarea unor seturi de date din ce în ce mai mari.
Eficiența se referă la modul în care un algoritm folosește resursele sistemului pentru a produce un rezultat. Resursele de interes sunt, în principal, timpul și memoria.
În cadrul analizei Big O, ne punem următoarele întrebări:
- Cum evoluează consumul de memorie al algoritmului odată cu creșterea datelor de intrare?
- Cum se schimbă timpul necesar algoritmului pentru a genera rezultate, pe măsură ce dimensiunea datelor crește?
Răspunsul la prima întrebare este cunoscut sub numele de complexitate spațială, iar cel la a doua, complexitate temporală. Folosim o notație specifică, numită Notație Big O, pentru a exprima aceste complexități. Mai multe detalii vor fi oferite în acest ghid.
Cerințe Preliminare
Pentru a înțelege pe deplin acest ghid Big O, este necesară o bază solidă în algebră. De asemenea, deoarece exemplele vor fi oferite în Python, o înțelegere de bază a limbajului este utilă, deși nu este necesară scrierea de cod.
Cum se Realizează Analiza Big O
Această secțiune se concentrează pe metodologia analizei Big O.
Este esențial să reținem că performanța unui algoritm este direct influențată de structura datelor de intrare.
De exemplu, algoritmii de sortare se execută cel mai rapid când datele sunt deja sortate în ordinea corectă. Acesta este considerat cel mai bun caz. Pe de altă parte, aceiași algoritmi sunt mai înceți atunci când datele sunt ordonate invers, acesta fiind cel mai nefavorabil caz.
În analiza Big O, ne concentrăm exclusiv pe scenariul cel mai nefavorabil.
Analiza Complexității Spațiale

Să începem cu analiza complexității spațiale. Ne propunem să evaluăm cum crește utilizarea memoriei suplimentare a unui algoritm pe măsură ce volumul de date de intrare crește.
De exemplu, funcția de mai jos folosește recursivitatea pentru a itera de la n la zero. Complexitatea spațială este direct proporțională cu n, deoarece fiecare apel recursiv adaugă un nou cadru la stivă. Astfel, complexitatea este O(n).
def loop_recursively(n):
if n == -1:
return
else:
print(n)
loop_recursively(n - 1)
O implementare mai eficientă ar fi:
def loop_normally(n):
count = n
while count >= 0:
print(count)
count =- 1
În acest caz, folosim doar o singură variabilă suplimentară pentru a itera. Chiar dacă n crește, avem nevoie tot de o singură variabilă, ceea ce înseamnă o complexitate spațială constantă, notată O(1).
Prin comparație, am observat că bucla while este mai eficientă în utilizarea memoriei decât recursivitatea, acesta fiind obiectivul analizei Big O: evaluarea comportamentului algoritmilor în raport cu creșterea datelor de intrare.
Analiza Complexității Timpului

Analiza complexității timpului nu se referă la timpul total de execuție al algoritmului, ci la creșterea numărului de pași de calcul. Timpul real de execuție este influențat de diverși factori, greu de controlat. Prin urmare, ne concentrăm pe evoluția pașilor de calcul, presupunând că fiecare pas are aceeași durată.
Pentru a ilustra, să analizăm următorul exemplu: avem o listă de utilizatori cu ID și nume. Sarcina este să implementăm o funcție care returnează numele unui utilizator, știind ID-ul acestuia. Iată o posibilă implementare:
users = [
{'id': 0, 'name': 'Alice'},
{'id': 1, 'name': 'Bob'},
{'id': 2, 'name': 'Charlie'},
]
def get_username(id, users):
for user in users:
if user['id'] == id:
return user['name']
return 'User not found'
get_username(1, users)
Acest algoritm parcurge lista de utilizatori până când găsește utilizatorul cu ID-ul corespunzător. Pentru 3 utilizatori, algoritmul efectuează 3 iterații, pentru 10 utilizatori, 10 iterații. Prin urmare, numărul de pași este proporțional cu numărul de utilizatori, algoritmul având o complexitate temporală liniară. Totuși, putem îmbunătăți acest algoritm.
Să presupunem că, în loc de o listă, am stoca utilizatorii într-un dicționar. Atunci algoritmul ar arăta astfel:
users = {
'0': 'Alice',
'1': 'Bob',
'2': 'Charlie'
}
def get_username(id, users):
if id in users:
return users[id]
else:
return 'User not found'
get_username(1, users)
În această nouă versiune, indiferent de numărul de utilizatori, numărul de pași pentru a găsi un utilizator rămâne constant, ceea ce înseamnă o complexitate constantă. Numărul de pași de calcul nu variază în funcție de numărul de utilizatori.
Ce este Notația Big O?
În secțiunea anterioară am analizat complexitățile Big O, atât spațială cât și temporală, descriindu-le prin termeni precum liniar sau constant. Notația Big O este un mod formal de a exprima aceste complexități.
Notația Big O este reprezentată printr-un O urmat de paranteze, în care se află o funcție a lui n, care descrie complexitatea specifică. Complexitatea liniară este reprezentată de n, fiind notată O(n), iar cea constantă de 1, notată O(1).
Există mai multe tipuri de complexitate pe care le vom discuta în continuare. Pentru a determina complexitatea unui algoritm, urmați pașii de mai jos:
- Determinați o funcție matematică f(n) care exprimă numărul de pași de calcul sau spațiul de memorie utilizat de algoritm, unde n este dimensiunea datelor de intrare.
- Selectați termenul dominant din funcție, ținând cont de ordinea dominanței: factorial, exponențial, polinomial, pătratic, liniar-logaritmic, liniar, logaritmic, constant.
- Eliminați toți coeficienții din termenul dominant.
Rezultatul final reprezintă complexitatea algoritmului.
Exemplu:
Analizăm următoarea funcție Python:
users = [
'Alice',
'Bob',
'Charlie'
]
def print_users(users):
number_of_users = len(users)
print("Total number of users:", number_of_users)
for i in number_of_users:
print(i, end=': ')
print(user)
Calculăm complexitatea temporală Big O a acestui algoritm.
Mai întâi, definim o funcție f(n) care exprimă numărul de pași de calcul în funcție de dimensiunea de intrare n.
Funcția efectuează doi pași: unul pentru a calcula numărul de utilizatori și altul pentru a-l afișa. Apoi, pentru fiecare utilizator, funcția execută doi pași: afișarea indexului și afișarea numelui. Funcția care descrie cel mai bine pașii de calcul este f(n) = 2 + 2n, unde n este numărul de utilizatori.
Alegem termenul dominant, în acest caz, 2n (liniar), deoarece liniarul este mai dominant decât constanta. Funcția devine f(n) = 2n.
Ultimul pas este eliminarea coeficienților. Eliminăm coeficientul 2 și obținem f(n) = n. Aceasta este complexitatea algoritmului, care este O(n), complexitate liniară.
Diferite Complexități Big O
În această secțiune, vom discuta despre diferitele tipuri de complexități Big O și graficele corespunzătoare.
#1. Constant

Complexitatea constantă înseamnă că algoritmul folosește o cantitate fixă de memorie sau efectuează un număr fix de pași, indiferent de dimensiunea datelor de intrare. Aceasta este cea mai eficientă complexitate, deoarece performanța algoritmului nu este afectată de creșterea datelor. Complexitatea constantă este notată O(1).
#2. Logaritmic
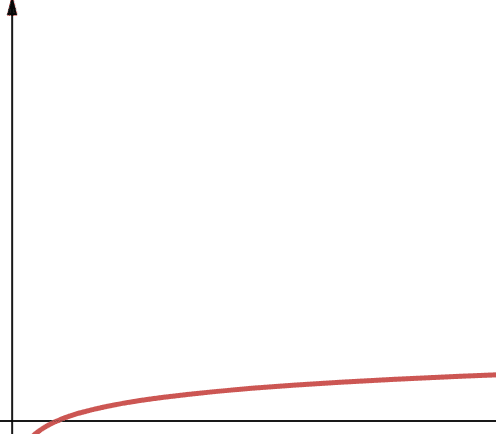
Complexitatea logaritmică este reprezentată de O(log n). În informatică, dacă baza logaritmului nu este specificată, se consideră implicit baza 2, adică log2n. Funcțiile logaritmice cresc rapid la început, dar încetinesc pe măsură ce n crește, scalând eficient.
#3. Liniar
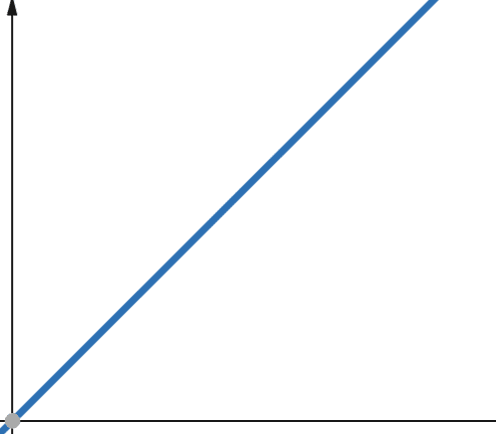
Într-o funcție liniară, creșterea variabilei dependente este direct proporțională cu creșterea variabilei independente. Complexitatea liniară, notată O(n), înseamnă că timpul sau spațiul alocat crește direct proporțional cu dimensiunea datelor de intrare.
#4. Linearitmic
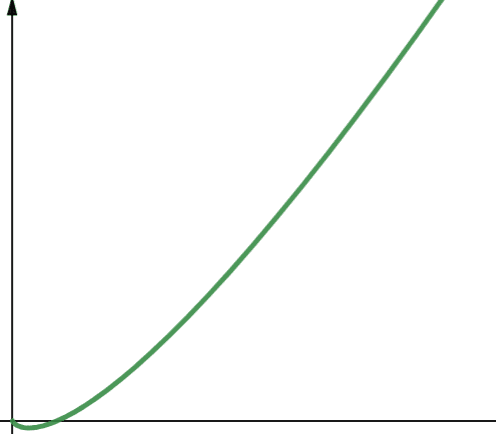
Complexitatea liniar-logaritmică este notată O(n * log n), fiind o combinație între funcția liniară și logaritmică. Funcțiile liniar-logaritmice sunt mai puțin scalabile decât cele liniare, deoarece log n este mai mare decât 1 pentru majoritatea valorilor lui n (log2n este mai mare decât 1 pentru n > 2).
#5. Pătratic
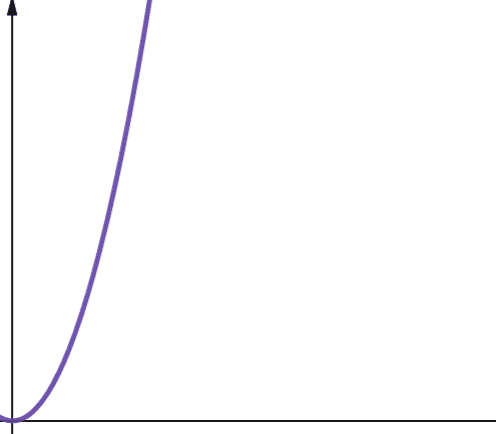
Complexitatea pătratică este reprezentată de O(n²). Dacă dimensiunea datelor de intrare se înmulțește cu 10, numărul de pași sau spațiul necesar crește de 10², adică de 100 de ori. Algoritmii cu complexitate pătratică sunt, în general, mai puțin scalabili.
#6. Polinomial
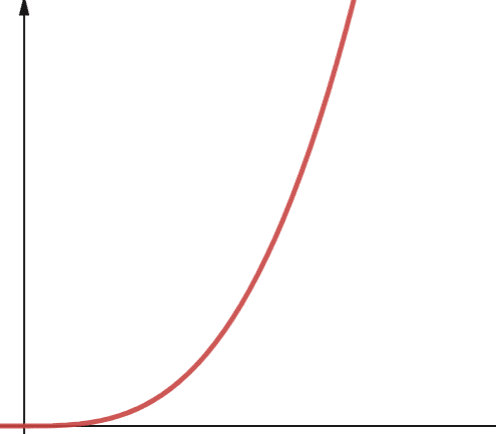
Complexitatea polinomială este reprezentată de O(n^p), unde p este o constantă întreagă. Diferența dintre complexitatea pătratică și polinomială constă în ordinul lui n. Complexitatea pătratică este un caz particular al complexității polinomiale, când p=2.
#7. Exponențial
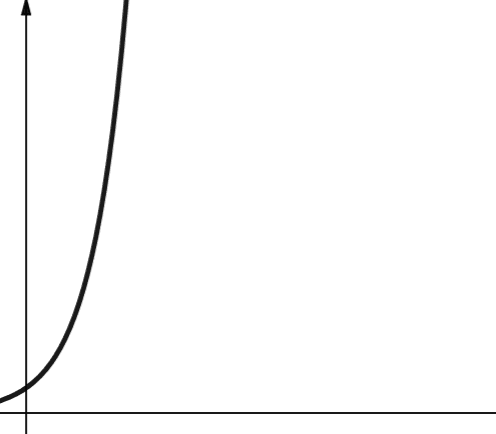
Complexitatea exponențială, notată O(2^n), crește foarte rapid odată cu dimensiunea datelor de intrare. O creștere cu 1 a lui n va dubla numărul anterior, ceea ce face ca acești algoritmi să fie extrem de nescalabili. În informatică, baza implicită a funcției exponențiale este 2.
#8. Factorial
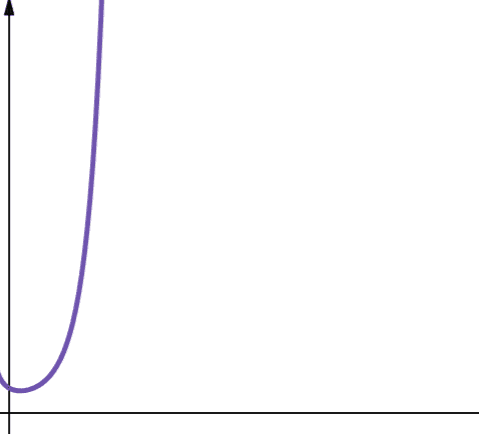
Complexitatea factorială, O(n!), crește rapid, fiind și ea nescalabilă.
Concluzie
Acest ghid a explicat analiza Big O și modul în care aceasta se calculează. Am discutat despre diferitele tipuri de complexități și implicațiile lor asupra scalabilității algoritmilor. Pentru aprofundarea înțelegerii acestor concepte, vă recomandăm să exersați analiza Big O pe diferiți algoritmi, cum ar fi algoritmii de sortare.